You have 50 minutes to complete this exam. This exam is worth 100 points. Use the back to continue your answers, if necessary.

1) Consider the following energy expression for a hypothetical molecular mechanics force field:

           A            B               C             D         E

a) For each of the summed terms in the above expression (A - E), identify which physical property is being captured. (15 points)

A: bond stretching

B: angle bending

C: torsion (dihedral twisting), specifically bond-bond repulsion (not required to say this for full credit).

D: van der Waals term for dispersion and repulsion, in the form of a Lennard-Jones 6/12 potential (did not have to identify name of potential).

E: Coulombic term to describe electrostatic nuclear interactions.

b) Consider the following molecule, and only the first three terms of the above force field expression for the next three questions (i, ii, and iii).

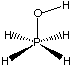
i) Do any of the first three terms require modification of their general form to properly model this molecule? If so, which term(s), and what modification(s) would you make? Do not concern yourself with anharmonicity (i.e. quadratic terms should be considered adequate). (15 points)

Consider the following figure:

Full credit for identifying that term C needs modification and that the modification must account for the four-fold torsional barrier. Conceptually, this can be done by replacing the cos3 w term with a cos4w term. No other terms require modification, and dipolar and hyperconjugative terms are not needed in this symmetrical molecule (recall R=H in problem 1 of problem set 1).

ii) What constants would be required in order to evaluate the energy for the H-O-P-H linkage in this molecule? You do not have to provide actual numbers for the constants, simply list them. For example, a calculation on H₂ using this force field would require r_e for H-H bonds. (5 points)

Need r_e and associated Ks for H-O, P-O and P-H bonds, q_e and associated Ks for H-O-P and O-P-H angles, and V_w for H-O-P-H torsion. Partial credit was earned if you identified some, but not all required constants. Since the example given was not complete, the Ks and V_w did not have to be identified to earn full credit.

iii) List three reasonable methods which might be used to obtain the constants you have listed for part ii). (5 points)

Any number of experimental or theoretical methods might be used. The best would involve some sort of structural spectroscopy (e.g. IR, NMR, x-ray, microwave, neutron, etc.). High-level theoretical calculations on model systems are also extensively used. Existing parameters for similar structures would be used only as a last resort. Regression fitting of "reasonable guess" parameters would also represent a desperate situation.

Note that electronic spectroscopy (e.g. UV/vis, ESR, etc.) is of limited value for this exercise.

Partial credit was given for identifying one or two methods, but not three.

2) What is the only situation in which it is appropriate to compare the molecular mechanics energy (e.g. the MMX energy) of two molecules? (10 points)

Only when the two molecules are conformational isomers. Period. In other words, only when you have the same atom types, same number of atoms and the same connectivity. Partial credit was earned for recognizing most, but not all of these conditions. In all other cases, heats of formation must be compared.

3) The general quantum mechanical Hamiltonian has the form:

What is the central approximation of quantum chemistry which allows us to completely ignore the first term and calculate only once (for any given geometry) the last term in the general Hamiltonian. Provide the name and a brief explanation of the rationale behind the approximation. (15 points)

This is the Born-Oppenheimer approximation. The rationale is that, since the nuclei are 1800 times more massive than the electrons, they move much slower, and we can treat the nuclei as frozen relative to the electrons. Hence, nuclear kinetic energy goes to zero, and r_kl in the last term becomes a constant.

To earn full credit, you must have given me the name, and recognized that the mass (or size) differential is the crucial part of the rationale.

4) Consider the following z-matrix:

AM1
Chem3D guess
C 0.000000 0 0.000000 0 0.000000 0 0 0 0
C 1.500000 1 0.000000 0 0.000000 0 1 0 0
H 1.086029 1 119.702500 1 0.000000 0 1 2 0
H 1.086014 1 119.702500 1 218.449631 1 1 2 3
C 1.499985 1 59.999008 1 109.225327 1 2 1 3
H 1.086014 1 119.702500 1 250.772934 1 2 1 5
H 1.086044 1 119.702500 1 109.225327 1 2 1 5
H 1.086044 1 119.702500 1 250.769440 1 5 1 2
H 1.086044 1 119.700760 1 109.228821 1 5 1 2
0

a) Sketch the molecule depicted by this z-matrix. (15 points)

The molecule is cyclopropane. The 60° C1-C2-C5 angle should have been a clue. Note that not all bonds need to be indicated in the z-matrix. This is a feature of there being only 3N-6 independent variables (for any molecule). The C1-C5 bond distance is not independent.

Partial credit was given for getting the connectivity right, but not recognizing the correct geometry.

b) There are two significant problems with this z-matrix. What are they? (10 points)

1) No symmetry was used, even though cyclopropane has D_3h symmetry.

2) This cyclic system was defined in such a way that the (undefined) C1-C5 bond distance is highly dependent on variables for C1 and C2. This is the "crack-the-whip" problem.

c) Explain how you would construct a more appropriate z-matrix. You do not have to write out your new z-matrix. Simply provide me with an indication of how you would do so. (10 points)

The best answer is to utilize dummy atoms as we did in class for benzene, and apply symmetry liberally. The dummy atoms will allow us to avoid the "crack-the-whip" problem, while the symmetry will provide a proper representation of the molecule and also reduce the computer time required for this optimization.

A good z-matrix for cyclopropane (see pages 109 and 320 in Clark):

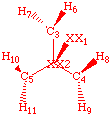
AM1 SYMMETRY

D3h cyclopropane

XX 0.0 0 0.0 0 0.0 0 0 0 0
XX 5.0 0 0.0 0 0.0 0 1 0 0
C 0.9 1 90.0 0 0.0 0 2 1 0
C 0.9 0 90.0 0 120. 0 2 1 3
C 0.9 0 90.0 0 240.0 0 2 1 3
H 1.0 1 122.0 1 0.0 0 3 2 1
H 1.0 0 122.0 0 180.0 0 3 2 1
H 1.0 0 122.0 0 0.0 0 4 2 1
H 1.0 0 122.0 0 180.0 0 4 2 1
H 1.0 0 122.0 0 0.0 0 5 2 1
H 1.0 0 122.0 0 180.0 0 5 2 1
0
3,1,4,5
6,1,7,8,9,10,11
6,2,7,8,9,10,11