Winter Quarter 1996

( Answer Key )

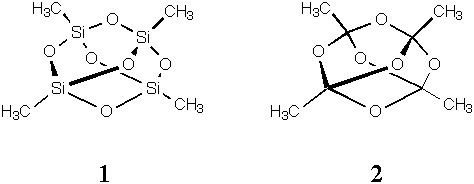
Using PC Model, answer the three questions below.

1. Energy minimize the structures of MeCuCN, MeAgCN, and MeAuCN. What are the three heavy atom bond lengths in each of these molecules? Do the structural results seem reasonable? Why or why not? In the breakdown of the MMX energies, you will note that many of the terms are exactly zero--why is that?

The lengthening of M-C bonds on going from copper to silver is reasonable. However, it stretches the imagination a bit to assert that the structures of the silver and gold complexes are identical! As for the lack of stretching strain, bending strain, etc., these molecules are so simple that they can indeed have all of their bond lengths and angles take on ideal (equilibrium) values. So, we can see that the parameter for the ideal Ag-CH₃ bond length is exactly the same as the one for the ideal Au-CH₃ (seems hard to believe, no?), etc. We may come back to these molecules with more sophisticated levels of theory and ascertain the reliability of the force field calculations.

2. When an amino acid is capped at its N-terminus with an acetyl group and its C terminus as an N-methyl amide, it is referred to as a dipeptide; i.e., the alanine dipeptide is drawn below as its fully extended conformer. In a non-polar environment (e.g., in the hydrophobic interior of a protein) the alanine dipeptide prefers to hydrogen bond one amide to the other to create a seven-membered ring. When this happens, the methyl group may either be disposed in a pseudoequatorial or pseudoaxial position (C7_eq and C7_ax conformations). These dipeptide ring conformers are equivalent to g turns found in protein secondary structure (g turns are possible connections between antiparallel b sheets). What are the relative energies of these three conformers assuming PC Model mimics a hydrophobic environment? Now consider the unnatural amino acid t-leucine (replace the methyl group in alanine with a t-butyl group). What are the relative energies of the three corresponding conformers of t-leucine? Based on your results, would you expect t-leucine to be more or less likely than alanine to be found at the corner of a g turn in an enzyme? (Note: be careful about hydrogen bonding in PC Model -- it's easy to accidentally turn it off!)

MMX (relative) energies, kcal/mol

Interestingly, turning the methyl group into a t-butyl group does not significantly increase the relative energy of the C7 structure where the alkyl residue is pseudo-axially disposed. This is predominantly because so many of the atoms in the seven-membered ring are not tetrahedral (i.e., no other axial substituents with which to have bad interactions). However, the relative energy of the extended conformer is lowered considerably in t-leucine. As a result, there is less energetic cost to not make a g turn, and one would probably expect to see fewer such turns at this residue than at alanine, all other things being equal. (Obviously, in a real protein one must also consider all of the other secondary structure as well, which is why it remains so challenging to predict protein folding patterns.)

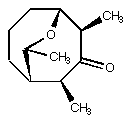
3. The natural product shown below inspires mayflies to stand on their heads. It is thus an important target for total synthesis. You have made it (optically pure, of course). On cooling your NMR tube to -80° C, you observe two separate pairs of doublets of quartets in the region of the ¹H NMR corresponding to protons alpha to a carbonyl. In one pair, the doublet splittings are 1.1 and 3.7 Hz, respectively, while in the other pair, the doublet splittings are 1.2 and 1.8 Hz, respectively (all quartet splittings are about 7 Hz). Answer the following two questions: (a) why are there two pairs of doublets of quartets? (b) what is the integration ratio of one pair compared to the other (e.g., 50:50, 80:20, etc?) Support your answer with data from PC Model.

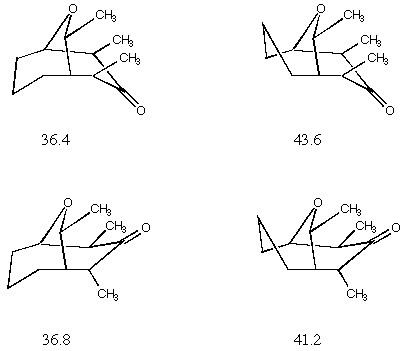
I found four stationary (i.e., all forces zero) conformers for this molecule which are illustrated below in schematic fashion (the molecules are a bit too complex for all-atom models to be sufficiently clear) The calculated MMX energies are also listed.

Note that flipping the left side of the ring is very costly, but the right side is not because of a balance between different steric interactions. Moreover, if one examines the predicted coupling constants for the protons alpha to the carbonyls (which should indeed be doublets of quartets) one discovers the lowest energy conformer to have doublet splittings of 1.14 and 3.70 and the conformer lying 0.4 kcal/mol higher to have doublet splittings of 1.17 and 1.81. Since both are observed, at the experimental temperature they must be present in equilibrium with a barrier to interconversion that is sufficiently high for isomerization to be slow on the NMR time scale.

As for the integration ratio, recalling the formula for a Boltzmann distribution, the fraction of a conformer A in an equilibrium mixture may be calculated as

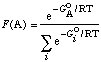(1)

where the lower sum runs over all equilibrium contributors (we'll make the approximation that the free energy will be the same as the MMX energy). Using the energies illustrated above and the experimental temperature of 193 K, one calculates a ratio of the four isomers of 71:29:(5.7x10^-07):(2.5x10^-05). Since your spectrometer isn't quite up to a 10⁶ signal to noise ratio, you don't see the other two conformers.