Using PC Model, answer any two of the three questions below.

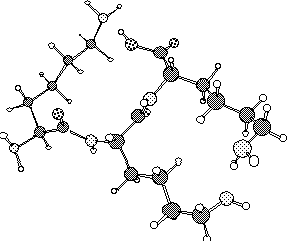
1. PCModel includes a number of substructure menus designed to facilitate the building of biopolymers. From the amino acid menu, construct the oligopeptide lys-lys-lys. In a biological system the C terminus would be deprotonated and the N terminus protonated, but let's not worry about that. The objective of this problem is to find the lowest energy conformation you can for this tripeptide. Presumably this will involve some internal hydrogen bonds. Grading will be based on the range of energies found (lower is better). When you have found what you think to be the lowest energy structure, print it out using the print option that includes the energy-try to orient your structure and choose the display option (e.g., ball-and-stick, tube, etc.) so as best to illustrate the actual conformation. [Note: On the Macintosh, some versions of PCModel will not send the PostScript file to the printer until you bring the Finder to the forefront, e.g., by touching the desktop.]

The above structure, which contains 2 internal hydrogen bonds, has an energy of -11.773 kcal/mol. It is certainly possible that there are lower energy structures.

2. Use the dihedral driver option in PCModel to construct torsional potentials about the indicated bonds in the three molecules below. Construct the potentials over the range of 180 degrees taking points every 15 degrees (symmetry dictates that only 180 degrees are unique). Note that PCModel saves the 12 structures to a file, with their associated energies, so you can open any one of them to look at its energy and get the breakdown of that energy into its force field components by doing a single point. By analyzing the contributions of different force field terms to the total energy, provide a chemical explanation for any important differences you perceive between the three potentials.

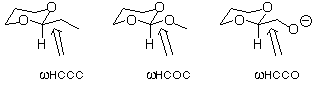
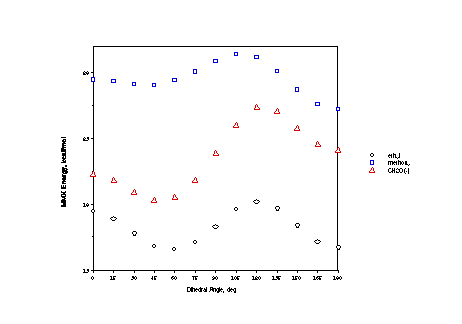
Table 1. Total variation in force field energies and components (kcal/mol).

Substituent	E	str	bnd	strbnd	tor	vdw	qq
Ethyl	3.699	0.112	0.427	0.063	1.886	1.284	0.008
Methoxy	4.202	0.126	0.838	0.056	2.405	0.958	1.456
CH2O-	7.040	0.177	0.948	0.064	2.830	1.452	4.803

The variations in bond stretching terms and stretch/bend terms are much smaller than the total energy variations-bond lengths do not change much as a function of the dihedral angles, in this case. Bending terms are 5 to 10 times larger, but still relatively small compared to the overall energy changes, suggesting that angle changes are also fairly small as a function of the dihedral angle.

In the ethyl case, all rotamers have essentially the same electrostatic term (the atoms in an ethyl group are uncharged in MMX), and the torsional profile is about 60% in the specific torsional term and 40% in the van der Waals term. The van der Waals term is about the same in every case. This may at first glance seem surprising, since oxygen atoms are "smaller" than alkyl groups, but remember that C-O bonds are shorter than C-C bonds, so some atoms are closer together in the oxygenated system.

The torsional term shows a variation of about half the full energy in each case, however, the periodicity of this term is very different for the methoxy substituent than for the other two. As shown on the next page, the methoxy torsional term is dominated by a two-fold periodic (if plotted over 360 degrees) component, whereas the other two are dominated by three-fold periodicity. That is, hyperconjugation dominates the methoxy case (where the anomeric effect is operative) but sterics dominate the other two (where it is not).

Finally, in the case of methoxy and methyleneoxide, electrostatics make a non-trivial contribution to the rotation coordinate (about 30% and 70% of variation, respectively). The variation in this term tracks the molecular dipole moment closely. Not surprisingly, oxygen atoms bearing lone pairs, and thus partial or full negative charges, prefer to minimize their interactions!

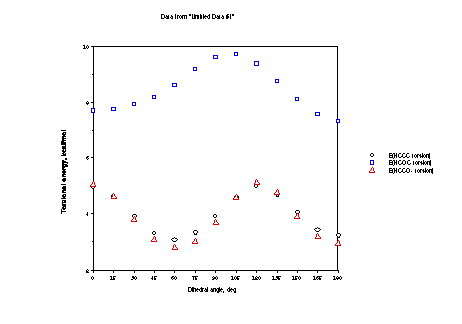
The net effect of the various points made above are that:

1) Ethyl shows typical gauche and trans minima with little difference in energy between the two.

2) Methoxy shows a deeper minimum for trans (maximal hyperconjugation) and shows a gauche minimum displaced from 60 in the direction of 0, and a very low barrier at 0, again because of hyperconjugation.

3) Methyleneoxide shows a deeper gauche minimum than trans because of the very unfavorable electrostatics for the latter. Those same electrostatics displace the gauche minimum from 60 in the direction of 0 and dictate a lower barrier at 0 than at 120.

3. Design a problem of your own that uses PCModel to illustrate some chemically interesting concept. Write down the problem, and then provide the answer. Note that you do not need to pick something that PCModel performs well for! However, if you create a problem where PCModel clearly gives the wrong prediction, provide some discussion in your answer of why the force field fails to be accurate. To get more of a feel for typical problems, feel free to drop by the website and look at first problem sets from previous years. Grading will be based on quality of the problem and originality.

Obviously, many answers are possible.

Important note on resources: In addition to the computers in 176 Kolthoff, there are platforms in the IT Labs that are running PC Model. In principle, you have access to these machines (assuming you've been assessed the IT computer fee-if you have any trouble, let me know). Locations are EE/CSci 3-170 (M-Th 7 am - 2 am; Fr 7 am - midnight; Sa-Su 10 am - 2 am) and Physics 130 (M-Th 8 am - 10 pm; Fr 8 am - 6 pm; Sa 10 am - 6 pm; Su 4 pm - 10 pm). For output you will need a printer access card, which can be obtained in the lab itself.