You will need to do the following in order for your Cray account
to work. You can begin the problem set at that point.
A. Telnet to sk.msc.edu (Macs in the microlab should have an NCSA Telnet macro that will get you there, or you can simply enter sk.msc.edu at the prompt after Open Connection in the File menu).
B. Provide your correct uid (e.g., me106**, whatever ** is for you).
C. The initial password on your account is ch#m8003. Enter these characters exactly.
D. You should now be logged in successfully, and you will be prompted to enter a terminal type. Unless you know you have a different kind of terminal, enter vt100 (this will probably be listed as the default). If you are using MacX to communicate, enter xterm (which will almost certainly be listed as the default).
E. To keep the news items from showing up every time you enter, type news, and scroll through using the space bar. Type q to end. You can read them if you are interested.
F. In order to change your password, enter the command passwd. You will first be asked for your old password (i.e., ch#m8003) and then be prompted for a new one. Enter a password of at least six characters, preferably with a number or special character in it (e.g., my@acct). You will be asked to re-enter it so as to verify you did not type it incorrectly the first time. If the two passwords match, your new password will be active next time-go on to step F. If you make a mistake at any point you will be dropped and ch#m8003 will remain the password. Repeat this step and type more carefully . . .
G. At the next prompt, type the following exactly: cp ../me10601/.cshrc . and hit return (that last "dot" is not a period to my sentence, it needs to be typed). You have now copied the script that will set up your shell when you log in from now on. Type csh to execute the script (this is the only time you will have to execute it yourself).
H. You're ready to roll! To run an AMSOL job you will need to have an input file named myfile.dat (where myfile is whatever you want, but .dat is critical). Remember, to create this you need to use the vi editor. You can either create a file directly while in vi, or go into input mode and paste something from the Mac. Once your input file is complete, type amsolb myfile (don't include the .dat suffix) and it will be submitted to the batch queue to run. You can check the queue by typing qsr-that will show you everything that is running presently (for more info about what everything means, you could type man qstat; qsr is aliased in your .cshrc to mean qstat -R.) When you don't see your job anymore, it is complete (although that doesn't necessarily mean it was successful!) If everything worked, you will have a myfile.out and myfile.arc file with the results of the run found therein (the .arc file is very condensed compared to the .out file). Note that the amsolb command limits your time in the queue to only about 3 minutes. None of the problems assigned should take that long, so if you run out of time, there is probably something wrong (a very bad geometry, for instance).
I. You can look at the output files by using more myfile.out, in which case it will scroll one page at a time, or by using vi, in which case you can use all of the editor commands to move around (be careful not to change the file, though).
J. When you log out, be careful to clean up old files you don't need (for instance, running AMSOL in batch creates files myfile.com*, myfile.qe, and myfile.qo-these can all be deleted). To delete a file, type rm filename. Be careful, though, once you rm a file, it's gone forever!
K. Your account has about 30 minutes of allocation (you can view
your allocation with the msiquery command).
Don't waste time! You need it to last you for the next problem
set too! On any day, you get 5 minutes of interactive time
(for editing, using Xmol, etc.), so don't try staying logged in
all day, as you'll eventually get booted.
The Problems: (note that there is an appendix to simplify
the compilation of some answers-written comments should still
be provided separately in several instances)
1. Use AM1 and PM3 to calculate the "heats of formation"
of the following molecules: F2, Cl2,
ClF, and ClF3. (i) Experimental heats of formation
are available for the first three molecules; locate the data and
decide which Hamiltonian is better for these calculations. Explain
your answer. (ii) An alternative method to evaluate the utility
of the methods is to calculate the enthalpy of reaction for F2
+ Cl2 t 2 ClF. Based on this approach, which
Hamiltonian is better and why? (iii) So, armed with this analysis
and any other data you can find, comment on your ClF3
calculations.
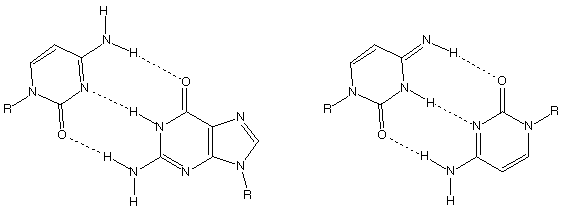
2. DNA replication must proceed with extremely high fidelity in
order to minimize the possibly disastrous effects of random base-pair
mismatches (i.e., mutations). At left below is the standard Watson-Crick
CG base pair. One possible source of mutations during DNA replication
is matching to tautomeric forms of the bases that are present
at equilibrium. For instance, the imino tautomer of cytosine can
form a strongly hydrogen-bonded reverse-Watson-Crick pair with
"normal" C (at right below). The frequency of such point
mutations is presumably related to the relative population of
imino-C compared to C during replication. Using AM1, calculate
the relative energies of these two tautomers of cytosine (take
R as a methyl group in order to keep things simple-you do not
need to include the other base in this calculation). At 298 K,
what is the ratio of normal tautomer to imino tautomer (assuming
AM1 energies to be free energies)? To be viable, organisms need
roughly part per million to part per billion fidelity in their
DNA replication. Should you be panicking? Why or why not? Please
attach your .arc file for each tautomer
to your completed problem set.

Normal C_G base pair Abnormal Im C_C Base Pair
3. The Diels Alder reaction of chlorocyclopentadiene (ccp)
and acrylonitrile (an) is shown below. The cycloaddition
may proceed to give two regioisomeric products (for simplicity,
we're going to consider only these products of endo cycloaddition,
and ignore the two exo possibilities).
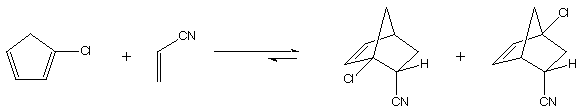
"ortho" "meta"
cycloadduct cycloadduct
pm3 tstate cycles=200 orthots.dat C 0.000000 0 0.000000 0 0.000000 0 0 0 0 -0.1579 C 1.407420 1 0.000000 0 0.000000 0 1 0 0 -0.1165 C 1.407388 1 108.222809 1 0.000000 0 2 1 0 -0.1337 C 1.401980 1 108.878497 1 0.655392 1 3 2 1 -0.0794 C 1.516806 1 107.421165 1 -19.325044 1 1 2 3 -0.0679 C 2.111649 1 98.126062 1 74.935865 1 1 2 3 -0.1074 C 2.192134 1 97.219388 1 -73.671052 1 4 3 2 -0.0540 H 1.090130 1 125.771391 1 176.630449 1 4 3 2 0.1145 C 1.424320 1 100.983452 1 -55.362859 1 7 4 3 -0.1074 H 1.107449 1 110.935221 1 -87.949048 1 5 1 2 0.0900 Cl 1.672221 1 124.240841 1 -171.008255 1 1 2 3 0.0721 H 1.089270 1 125.781035 1 165.511688 1 2 1 5 0.1304 H 1.103272 1 114.899884 1 151.455100 1 5 1 2 0.0835 H 1.091466 1 91.984616 1 168.985907 1 6 1 2 0.0878 H 1.089692 1 125.128040 1 -174.154754 1 3 2 1 0.1296 H 1.089675 1 97.550695 1 55.006343 1 6 1 2 0.0910 H 1.100839 1 91.146960 1 -170.046145 1 7 4 3 0.1149 Xx 5.000000 0 90.000000 0 180.000000 0 9 7 4 N 1.161237 1 89.492365 1 -179.267975 1 9 18 7 -0.0897 0 0.000000 0 0.000000 0 0.000000 0 0 0 0
Oversimplified, but nevertheless often useful, models have been
developed to predict regioselectivity in Diels Alder reactions
like this one. In particular, one begins by examining the highest
occupied and lowest unoccupied orbitals on the diene and dienophile
(i.e., HOMOs and LUMOs, which are nearly always the relevant pi
orbitals in these simple cases). One interaction occurs with a
smaller energy separation than the other, and is hence the most
relevant for a frontier orbital analysis. For a "standard"
Diels Alder reaction, it is the HOMO-diene/LUMO-dienophile interaction
(thus standard Diels Alder reactions are accelerated by pi donors
on the diene (raises HOMO energy) and pi acceptors on the dienophile
(lowers LUMO energy)). For an "inverse-electron-demand"
Diels Alder, it is the HOMO-dienophile/LUMO-diene separation that
is smallest. What are the HOMO and LUMO energies of ccp
and an? (You will need to include the VECTORS keyword in
your input file in order to have the molecular orbitals and their
energies printed.) Is this a standard Diels Alder reaction or
an inverse-electron-demand? Once you have the relevant HOMO and
LUMO, look at the orbital coefficients. Since the molecules are
planar, and the pi orbitals use only the out of plane p basis
functions, all of the coefficients in the HOMO and LUMO should
be zero (or very close to zero) except for the coefficients for
one kind of p function (probably pz). List
those coefficients for each atom in ccp and an.
The simplified models suggest that regioselectivity can be predicted
by comparing coefficients and matching the largest coefficient
for a diene terminus to the largest for the dienophile vinyl unit
(and, obviously, the smallest to the smallest). Does this work
in this case?
Appendix:
1.
| F2 | |||
| Cl2 | |||
| ClF | |||
| F2 + Cl2 --> 2 ClF | |||
| ClF3 |
Structure of CF3:
2.
3.
For the smallest HOMO-LUMO gap (label which orbital corresponds
to which molecule) list the pi coefficients (note that absolute
sign is arbitrary-only relative sign matters. That is, it doesn't
matter if your largest coefficient is negative on the acrylonitrile
vinyl unit but positive on a chlorocyclopentadiene terminus, those
are still the two centers that would be bonded to predict regioselectivity
using simple models).
Reaction is standard/inverse-electron-demand Diels Alder (circle
one).
Cytosine
Iminocytosine
Structure acrylonitrile
chlorocyclopentadiene
Structure ortho cycloadduct
meta cycloadduct
Structure ortho TS structure
meta TS structure