Chemistry 8003: Computational Chemistry

Winter Quarter 1997

( Due 2 / 17 / 97 )

Things to remember: To run an AMSOL job you will need to have an input file named myfile.dat (where myfile is whatever you want, but.dat is critical). Remember, to create this you need to use the VI editor. You can either create a file directly while in vi, or go into input mode and paste something from the Mac. Once your input file is complete, type amsolb myfile (don't include the .dat suffix) and it will be submitted to the batch queue to run. You can check the queue by typing qsr--that will show you everything that is running presently (for more info about what everything means, you could type man qstat; qsr is aliased in your .cshrc file to mean qstat -R.) When you don't see your job anymore, it is complete (although that doesn't necessarily mean it was successful!) If everything worked, you will have a myfile.out and myfile.arc file with the results of the run found therein (the .arc file is very condensed compared to the .out file). Note that the amsolb command limits your time in the queue to only about 3 minutes. None of the problems assigned should take that long, so if you run out of time, there is probably something wrong (a very bad geometry, for instance).

You can look at the output files by using more myfile.out, in which case it will scroll one page at a time, or by using vi, in which case you can use all of the editor commands to move around (be careful not to change the file, though--if you accidentally delete or change something, you can leave the file unaffected by entering :q! when in command mode).

When you log out, be careful to clean up old files you don't need (for instance, running AMSOL in batch creates files myfile.com*, myfile.qe, and myfile.qo--these can all be deleted). To delete a file, type rm filename. Be careful, though, once you rm a file, it's gone forever!

Your account has about 44 minutes of allocation (you can view your allocation with the msiquery command--we use machine sk, ignore the sr column). Don't waste time! You need it to last you for the next problem set too!

The Problems:

1. Use AM1 to calculate the barriers to inversion for NH3 and NH2F. One barrier is higher than the other. Explain why. To further your explanation, construct Walsh diagrams for the pyramidal minima going to planar transition state structures for each molecule. [A Walsh diagram is a pictorial representation of the changes in orbital energies during a geometric change.] We'll keep it simple, and just use the two structures we need for each barrier. To get the MO's, you will need to use the keyword VECTORS in your input decks. This causes the program to print out the coefficients for each MO near the end of the file. The last page provides an example for the inversion of water through its linear form that you may use to guide you. To sketch a molecular orbital, you need to adopt a convention for where you put the shading in s and p orbitals for positive coefficients (consistency is all that matters), and you need to add all of the basis set orbitals together according to their coefficients in that MO, and you need to make sure that you have the cartesian coordinates for the molecule so you know how the p orbitals relate to the atomic positions. [Modern programs will do all of this for you with glitzy graphics, but doing it by hand once or twice is good for the soul and provides more insight into what's going on.] Please label your MO's with the calculated MO energy.

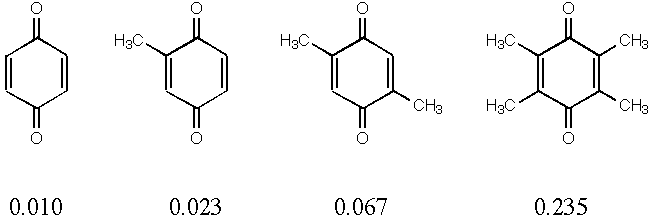
2. Quinones are used in many biological systems as one-electron acceptors in redox processes. Below are 4 quinones with their measured reduction potentials in eV. Reduction potential should correlate with the energy of the lowest unoccupied molecular orbital (LUMO)--the lower the LUMO energy, the easier it is to pump an electron in. Calculate the LUMO energies for the 4 quinones below and plot against the reduction potential to get a best fit line. Now calculate the LUMO energy for trimethylquinone and use your fit to predict its reduction potential. How does that compare to the measured value of 0.165 eV?

3. Cubane is a fascinating molecule for a variety of reasons. It has an isomer that can be considered to be aromatic (6 p electrons in double bonds, 4 p electrons in methylene bridges). What is the difference in predicted heats of formation at the PM3 level? Is that stability what you expected? Now, what if we replace every carbon atom with silicon, what is the difference in stability? Is that result what you expected?




Inversion of Water through Its Linear Form

Water molecule, minimum energy geometry:

     1        O             0.00000   0.00000   0.00000
     2        H             0.59492   0.75494   0.00000
     3        H             0.59492  -0.75494   0.00000

so, the coordinate axes can be viewed as:

I'll use the convention that whenever I see a p orbital with a positive coefficient, that means the shaded lobe should point in the positive cartesian direction, and that a positive s is also shaded.

Here are the vectors for waters 4 occupied orbitals (notice that the sum of the squares of the coefficients in any MO adds to 1.0, just as it should!):

    ROOT NO.    1           2           3           4   

           -36.10883   -17.92790   -14.55189   -12.01203


   S O   1  -0.89339     0.00000    -0.36499     0.00000
  PX O   1  -0.15803     0.00000     0.80115     0.00000
  PY O   1   0.00000    -0.77017     0.00000     0.00000
  PZ O   1   0.00000     0.00000     0.00000    -1.00000

   S H   2  -0.29740    -0.45102     0.33536     0.00000

   S H   3  -0.29740     0.45102     0.33536     0.00000

The first number is the energy of the orbital (in eV) -- it gives a quite reasonable estimate of the ionization potential from this orbital (that results is called Koopman's theorem). That energy is sometimes called the "eigenvalue" of the MO (which is itself an "eigenvector" of the secular matrix).

So, to sketch orbital one, I take a non-shaded s orbital (the coefficient is negative, and my convention is shaded is positive) with a big weight. I add a little bit of a px orbital (small coefficient) and I put the shaded part pointing to the negative x direction (my convention is that if the coefficient is positive, I put the shaded part in the positive direction, but this coefficient is negative). I then add some non-shaded s orbitals on each H with moderate weight. The pieces are shown at right, the sum (which just involves adding the oxygen orbitals together) is:

This is the lowest energy (valence) orbital for water, and properly has the same symmetry as the molecule (C2v). The other can be similarly constructed. The resulting Walsh diagram after doing this for all the other orbitals for water and linear water (TS structure for inversion) is shown below. Note, for instance, that water itself has two distinct lone pairs, one in plane, and one out of plane of higher energy. This is confirmed by photoelectron spectroscopy, and reflects one of the most annoying lies undergraduates are told (i.e., water has two identical sp3 lone pairs).

Interpreting the Walsh diagram, one would say that the dominant contribution to the inversion barrier is the rise in energy of orbital 3 (owing to loss of s character).