Chemistry 8003: Computational Chemistry

Winter Quarter 1997

( Due 2 / 17 / 97 )

The Problems:


1. Use AM1 to calculate the barriers to inversion for NH3 and NH2F. One barrier is higher than the other. Explain why. To further your explanation, construct Walsh diagrams for the pyramidal minima going to planar transition state structures for each molecule. [A Walsh diagram is a pictorial representation of the changes in orbital energies during a geometric change.] We'll keep it simple, and just use the two structures we need for each barrier. To get the MO's, you will need to use the keyword VECTORS in your input decks. This causes the program to print out the coefficients for each MO near the end of the file. Please label your MO's with the calculated MO energy.

The barrier to inversion for NH3 is 4.2 kcal/mol, while it is 12.2 kcal/mol for NH2F.

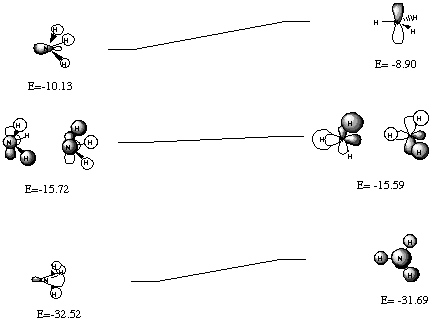
The Walsh diagram is shown below:

NH3 Walsh Diagram


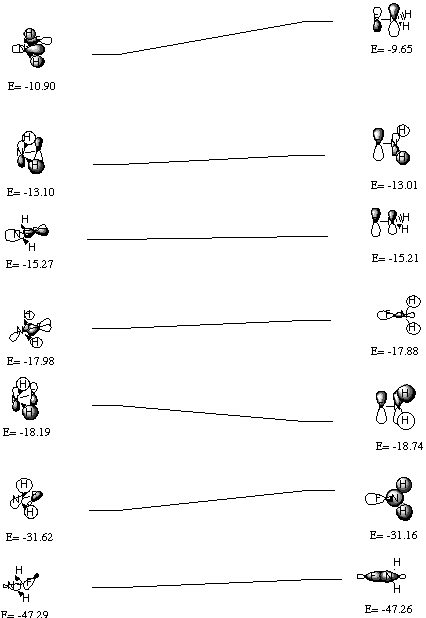
The Walsh diagram for NH2F is below:

NH2F Walsh Diagram



The classical explanation for the larger inversion barrier in the fluorosubstituted ammonia is that the more electronegative substituent (fluorine) destabilizes the planar transition state because it withdraws electron density more efficiently from nitrogen (the nitrogen hybridization of the NF sigma bond is sp2 in the TS, but sp3 in the reactant). The Walsh diagrams do not provide much support for this, as perhaps they should not (why worry about nitrogen? Why not think of it from fluorine's point of view and figure that is a stabilizing interaction?) The problem appears to be one more associated with electron correlation, and probably requires a deeper analysis than is expected for this problem set.

2. Quinones are used in many biological systems as one-electron acceptors in redox processes. Below are 4 quinones with their measured reduction potentials in eV. Reduction potential should correlate with the energy of the lowest unoccupied molecular orbital (LUMO)--the lower the LUMO energy, the easier it is to pump an electron in. Calculate the LUMO energies for the 4 quinones below and plot against the reduction potential to get a best fit line. Now calculate the LUMO energy for trimethylquinone and use your fit to predict its reduction potential. How does that compare to the measured value of 0.165 eV?

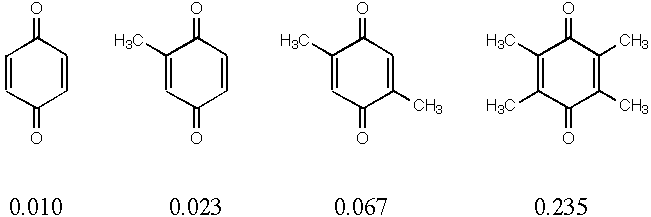
Various Quinones


MoleculeLUMO Energy (eV) Red. Potential (eV)
Quinone-1.67 0.010
Methylquinone-1.57 0.023
Dimethylquinone-1.48 0.067
Tetramethylquinone-1.34 0.235

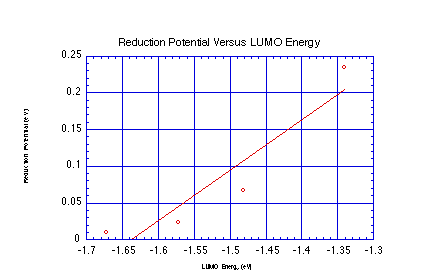
Red. Pot. vs. LUMO Energy


Linear Regression over Data Set:
Slope: 0.688
Intercept: 1.128
For Trimethylquinone:
Calculated LUMO Energy: -1.41 eV
Predicted Reduction Potential: 0.161 eV
Actual Reduction Potential: 0.165 eV

This shows that the LUMO energy does a pretty good job of predicting the reduction potential. A linear regression is warranted based strictly on unit analysis (eV vs eV), but one could also justify interpolation (which doesn't change the answer much). Higher order fits are probably not warranted, although again they wouldn't change the answer much.

3. Cubane is a fascinating molecule for a variety of reasons. It has an isomer that can be considered to be aromatic (6 p electrons in double bonds, 4 p electrons in methylene bridges). What is the difference in predicted heats of formation at the PM3 level? Is that stability what you expected? Now, what if we replace every carbon atom with silicon, what is the difference in stability? Is that result what you expected?

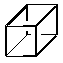vs.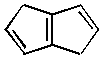
ElementDHf (kcal/mol) DHf (kcal/mol)
C113.856.1
Si18.1108.4

All-carbon cubane is very unstable, in part because carbon does not like 90o angles. Silicon, on the other hand, easily accomodates small bond angles, and persilacubane turns out to the the lowest-energy isomer of Si8H8. For a number of reasons, including long bond lengths,p overlap is poor for the persilabicyclooctatriene, while it is fine for carbon. All of these effects together account for the 150 kcal/mol (!) difference in relative energies for these two species.