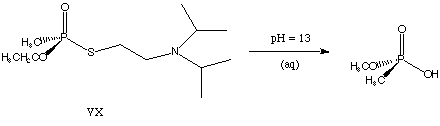
1a)
Table 1.1: Heats of Formation, Computed and Experimental (kcal/mol)
| H2 | C2H2 | C2H4 | C2H6 | C6H6 | |
|---|---|---|---|---|---|
| MNDO | 0.7 | 57.9 | 15.4 | -19.7 | 21.3 |
| Error | + 0.7 | 3.4 (6.2%) | 2.9 (23%) | 0.3 (1.5%) | 1.6 (8.1%) |
| AM1 | -5.2 | 54.8 | 16.5 | -17.4 | 22.0 |
| Error | - 5.2 | 0.3 (0.6%) | 4.0 (32%) | 2.6 (13%) | 2.3 (12%) |
| PM3 | -13.4 | 50.7 | 16.6 | -18.1 | 23.5 |
| Error | - 13.4 | 3.8 (7.0%) | 4.1 (33%) | 1.9 (9.5%) | 3.8 (19%) |
| Exp. | 0.0 | 54.5 | 12.5 | -20.0 | 19.7 |
Table 1.2: Enthalpies of Hydrogenation, Computed and Experimental (kcal/mol)
| H2 + C2H2 --> C2H4 | H2 + C2H4 --> C2H6 | |
|---|---|---|
| MNDO | -43.2 | -35.8 |
| Error | -1.2 (2.9%) | -3.2 (9.8%) |
| AM1 | -33.1 | -28.7 |
| Error | 8.9 (21%) | 3.9 (12%) |
| PM3 | -20.7 | -21.3 |
| Error | 21.3 (51%) | 11.3 (35%) |
| Exp. | -42.0 | -32.6 |
In both cases, MNDO gives the best overall agreement. This should seem odd, since MNDO was the first of the three to be developed. The main reason for this probably lies in the philosophy taken while developing AM1 and PM3. That is, the parameterization set focused more on larger molecules containing heteroatoms. These molecules are all small enough to be treated with high-quality ab inito theory. It is distressing to see how poorly even our "best" semiempirical Hamiltonians perform, though.
b)
Table 1.3: C-C Bond Lengths, Computed and Experimental (Å)
| C2H2 | C2H4 | C2H6 | C6H6 | |
|---|---|---|---|---|
| MNDO | 1.195 | 1.335 | -1.521 | 1.407 |
| Error | -0.008 (0.7%) | -0.004 (0.3%) | 0.014 (0.9%) | 0.008 (0.6%) |
| AM1 | 1.195 | 1.326 | -1.500 | 1.395 |
| Error | -0.008 (0.7%) | -0.013 (1.0%) | 0.035 (2.3%) | 0.004 (0.3%) |
| PM3 | 1.190 | 1.322 | -1.504 | 1.391 |
| Error | -0.013 (1.1%) | -0.017 (1.3%) | 0.031 (2.0%) | -0.008 (0.6%) |
| Exp. | 1.203 | 1.339 | 1.535 | 1.399 |
a) Experimental data from the CRC handbook,
73rd Edition, "Bond Lengths and Angles in Gas-Phase Molecules",
pp 9-15-9-41.
Once again, MNDO gives the best overall agreement, although all three Hamiltonians are acceptably close to the experimental (gas-phase) results. This emphasizes the fact that geometries are much easier to calculate than energies.
a) + b)
Based on this problem, MNDO looks like the best. I don't believe that. One philosophy is to try a number of Hamiltonians, and then pick the one that best reproduces the quantity you want. Since different philosophies are used to parameterize the Hamiltonians, it is unlikely that you will ever find a single Hamiltonian that is best in every situation.
One comment about the "heat of formation" reported by semiempirical programs. Quantum mechanically, H = E + ZPVE. But, the "heat of formation" reported by AMSOL does not correspond to this equation. It is a type of electronic energy (E), but has no vibrational correction (ZPVE). It is called a "heat of formation" because experimental heats of formation are used in the parameterization of Hamiltonian.
2) Corrected
structure for VX. (I had a methoxy group where an ethoxy group
belongs).
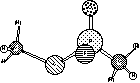
Your structures should look something like:
 |
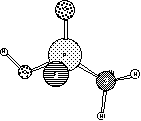 |
They both look quite reasonable with tetrahedral phosphorus. If you noticed the atomic charges, though, you would see that P is fairly positive, while O is fairly negative. This indicates that the double bond is highly charge-separated, and is a symptom of the problem we are about to uncover.
The trigonal bipyramidal structure should have come out looking something like (even stranger structures might have been found):
The water has migrated away from the phosphorus, allowing the P to return to a tetrahedral hybridization by shedding one ligand. The reason for this is the lack of d orbitals in the AM1 (or PM3 or MNDO for that matter) Hamiltonian. Hypervalency requires d orbitals for proper hybridization, so this calculation fails. That is also why the P-O double-bond is so polarized. A true double-bond would require 5 bonds to P, even though it's still tetrahedral. We can only make four with and s and p basis.
3)
a)
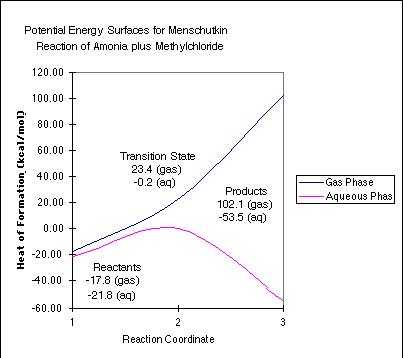
In the gas-phase, the "barrier"
is 41.2 kcal/mol, but the entire reaction is endothermic
by 119.9 kcal/mol. A number of you questioned whether the gas-phase
structure is truly a transition state. It is. If we looked hard
enough, we could find a minimum between the transition state and
the isolated products that corresponds to an ion-dipole complex
that is only stable in the gas phase.
In the aqueous phase, the barrier is 21.6 kcal/mol, and the overall reaction is exothermic by 31.7 kcal/mol. The neutral reactants are only slightly solvated, while the transition state, with it's nascent charge development, is stabilized by more than 23 kcal/mol. Finally, the charged products are stabilized tremendously by solvation, leading to the observed result.
These numbers are in good agreement with experiment. See Gao and Xia, J. Am. Chem. Soc. 1993, 115, 9667 - 9675.
b)
ROT=3 tells the program that we have three-fold symmetry on the principle rotation axis. This information is needed to compute the entropic corrections to the energy. TRANS=1 tells the program that this is a transition state, so it should ignore the lowest vibration (i.e. the negative one) when computing the vibrational corrections to the energy.
You should have found a negative mode of approximately -654 wavenumbers. The atom motions are primarily C-N and C-Cl stretching (0.95 and 0.81 Å, respectively) and the CH3 umbrella motion (H shift of 0.98 Å). This is exactly what we would want to see for this transition state.
I ran an IRC on this transition state at the HF/3-21G level of theory.
The IRC Animation is here.
If there is a problem, try this one (It has a bit smaller screen size
so the buttons work on my Mac.)