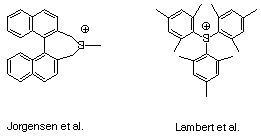
| Chemistry 8003 | Computational Chemistry | 4 Credits | Winter Quarter 1999 | ( Due 2 / 15 / 97 ) |
Things to remember: To run an AMSOL job you will need to have an input file named myfile.dat (where myfile is whatever you want, but .dat is critical). Remember, to create this you need to use the vi editor. You can either create a file directly while in vi, or go into input mode and paste something from the Mac. Once your input file is complete, type amsoli myfile (don't include the .dat suffix) and it will be submitted to run interactively. When the prompt returns, your run is complete (although that doesn't necessarily mean it was successful!) If a job seems to be running a long time, you probably made some sort of mistake (a very bad geometry, for instance), and you should ^C to interrupt the process and look at whatever output file may have been created to see what you did wrong. If everything worked well, you will have a myfile.out and myfile.arc file with the results of the run found therein (the .arc file is very condensed compared to the .out file).
You can look at the output files by using more
myfile.out, in which case it will scroll one page at a
time, or by using vi, in which case
you can use all of the editor commands to move around (be careful
not to change the file, though-if you accidentally delete or change
something, you can leave the file unaffected by entering :q!
when in command mode).
The Problems (do any two of three):
1. Jorgensen et al. reported in JACS 120 (1998) 7637 the synthesis
of a tertiary silicenium ion in solution. This assignment is almost
certainly wrong (even JACS referees aren't perfect!)-silicenium
ions are terrifically unstable compared to carbonium ions. Indeed,
the only unambiguously established silicenium ion, tris-mesitylsilicenium
(made by Lambert et al.), owes its stability primarily to steric
crowding about silicon, not aryl stabilization; triphenylsilicenium
cannot be formed in solution. This is in marked contrast to triphenylcarbenium,
which is rock stable, and begs the question of: Why doesn't aryl
substitution stabilize a silicenium ion like it does a carbenium
ion?
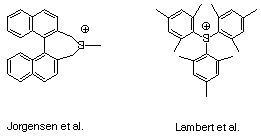
To answer this question more fully, let's look at the MOs for
phenyl carbonium (PhCH2+) and phenylsilicenium
(PhSiH2+). Optimize the structures of these
two cations at the AM1 level. To get the MO's you will need to
use the keyword VECTORS in your input decks. This causes the program
to print out the coefficients for each MO near the end of the
file. In the NDDO approximation, recall that the sum of the squares
of all coefficients of a MO is 1, so the square of the coefficient
tells you the percentage contribution of each AO basis function
to a given MO. Sketch the p MO's (how
many are there?) noting the percentage contribution of each AO
to the MO. To sketch a molecular orbital, you need to adopt a
convention for how you shade the orbitals for positive vs. negative
coefficients (consistency is all that matters), and you need to
make sure that you have the cartesian coordinates for the molecule
so you know how the orbitals relate to the atomic positions, and
you need to scale your various atomic orbitals according to the
MO coefficients, i.e., a big coefficient means lots of that atomic
orbital, a small coefficient means just a little bit of that atomic
orbital, and finally, of course, you need to know which atom is
which in your input deck! [Modern programs will do all of this
for you with glitzy graphics, but doing it by hand once or twice
is good for the soul and provides more insight into what's going
on.] Label your MO's with the calculated MO energy. If any of
these p MOs correspond to the HOMO
or the LUMO, so label them. Notice anything you think strange
about the LUMO energies?
Also report the partial atomic charges on the carbonium carbon
and the silicenium silicon. With all your analysis in hand, why
is an aryl silicenium ion so much less stable than its
analogous carbonium ion?
MO pictures and energies (in eV) and AO contributions can be
found on the next page. There are 7 ptype
MO's, although number 4 is formally non-bonding. The HOMO and
LUMO are 3 and
4, respectively. The LUMO has a negative energy, which
is mildly unusual for a neutral (implies that adding an electron
would be a favorable process-typical neutrals do not have negative
energies for electron affinities) but perfectly reasonable for
a cation. Indeed, all of the p-type
orbitals have negative energies (eigenvalues) reflecting how much
nature hates a charge in the gas phase.
In a nutshell, these two systems differ so significantly because
a silicon 3p orbital fails to mix as effectively as a carbon 2p
orbital with an attached benzene p
system (which is itself, of course, also formed from carbon 2p
orbitals). Thus, 76% of the non-bonding LUMO in phenylsilicenium
is the silicon p, but only 44% of the same orbital in phenylcarbenium
is the carbon p. In other words, charge is more delocalized in
the acceptor LUMO. Notice also that since we have all the
p orbitals here, the sum of any one
AO's contributions to all the p orbitals
must be 1. Thus, we can ask how many electrons are on the cationic
atom by considering how much its p AO contributes to filled orbitals
compared to empty. With carbon, the ratio is 27% filled to 73%
empty. With silicon, it is only 15% filled to 85% empty-again,
one expects more positive charge to reside on silicon. The Mulliken
charges confirm this analysis: charge is 0.13 on carbon but a
whopping 1.38 on silicon! (The seemingly much larger difference
in charge than in total number of p
electrons reflects the importance of s
orbitals in the charge analysis.) Concentrated charge causes enormous
instability in chemical systems.
Note the interesting inversion in relative energies for p-type
orbitals 5 and 6 depending on the nature of the cationic atom.
Remember that the two sets of orbital energies are not really
on the same scale, since differences in the relative electronegativities
of carbon and silicon will be reflected in the absolute energies
for adding electrons to the system. Since carbon is more electronegative
than silicon, its orbitals are lower in energy than corresponding
ones in the other system.
[Some of you, exercising the powerful skepticism that characterizes
a scientist, may be wondering how the above problem can prove
that Jorgensen and co-workers are wrong. Of course it doesn't-it
just suggests why it's so hard to get a stable silicenium
ion. We'll defer more convincing proof until we can compute NMR
chemical shifts ab initio (next problem set).]
2. Let's return to one of the molecules found in Problem Set 1.
For the case of 2-methoxy-1,3-tetrahydropyran, MMX gave a rotational
potential consistent with a large anomeric effect. The anomeric
effect is a stereoelectronic effect, i.e., it derives from orbital-orbital
interactions. Repeat your calculations for this torsional potential
at the PM3 level.
AMSOL has a way to simplify the calculation of this potential.
Instead of flagging the dihedral angle with a "1" (meaning
optimize) flag it with a "-1". A -1 flag means to hold
that degree of freedom fixed at whatever the value is in the Z-matrix,
optimize everything else, and then repeat that process for every
value found on the line(s) following the first blank line after
the Z-matrix. All results are provided in a single output file
For instance:
AM1
phosphinous acid, rotation coordinate for P-O bond (gas phase)
O
P 1.5 1
H 1.3 1 115. 1
H 1.3 1 115. 1 120. 1 2 1 3
H 1. 1 110. 1 0. -1
3 1 2
30. 60. 90. 120. 150. 180.
would calculate the rotational potential for phosphinous acid
(H2POH) by 30 degree intervals starting from
zero.
Compare the PM3 potential to the MMX potential. What, if any,
are the differences? If there are important differences, what
could you do to establish which level of theory (if either) is
the more correct?
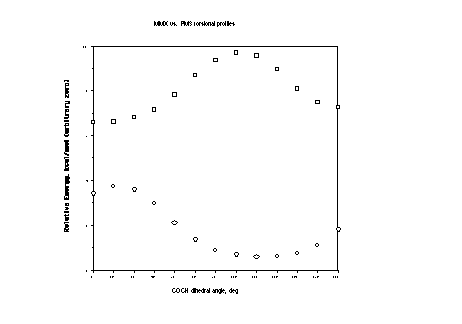
That comparison is shown graphically below using arbitrary zeroes of energy for the different levels; squares are MMX results, circles are PM3 results. Notice the enormous qualitative difference! Where PM3 says there is a global minimum is roughly where MMX puts the highest barrier on the torsional potential. Secondary minima are also significantly shifted in energy. Yuck.
As to what one might do to try and decide which, if either,
is correct, there are any number of possibilities, a few of which
are listed below, in rough order of preference.
1) Try to find some reasonably analogous system (dimethoxymethane?)
for which experimental data on the torsional potential are available
and benchmark both levels of theory against those data.
2) Move on to a higher level of theory to attempt to converge
the quantum mechanical results. We'll do this for Problem Set
3 and see if we can come to any conclusions.
3) Try AM1. If AM1 and PM3 disagree significantly, there is
more reason to doubt semiempirical theory. Similarly, try a few
different force fields. Is there a consensus amongst various lower
level theories?
4) Consider the parameterization sets. How carefully were
torsions like that found in our test system examined, if at all,
as part of the parameterization process?
5) What does the literature have to say, if anything, about
these kinds of modeling efforts? Have analogous systems been examined?
6) Trust in your hard-won intuition.
3. Design a problem of your own that uses semiempirical
MO theory to illustrate some chemically interesting concept. Write
down the problem, and then provide the answer. Note that you do
not need to pick something that semiempirical theory performs
well for! However, if you create a problem where NDDO theory clearly
gives the wrong prediction, provide some discussion in your answer
of why the level fails to be accurate. To get more of a feel for
typical problems, feel free to drop by the website and look at
second problem sets from previous years. Grading will be based
on quality of the problem and originality.
Obviously, many answers are possible.