Prolog II (or "How Do I Run This Infernal Program? Revisited"):
1) Telnet over to the Cray C-90 (sk.networkcs.com).
2) Your input files must be named something.ext, where "something" is whatever you want to call that particular job, and "ext" is whatever extension you want to use for your input. Use any three-letter extension you wish. Common extensions for input files include .dat, .com, .inp and .g94. Edit your files using your favorite method, honed to a fine skill by Problem Set 2.
3) Once your files are in place, you're ready to roll! To run a G94 job, you will simply type qrun something.ext, where you must include the extension. If you do not, the command will not be able to find your input. NOTE: This is different from what you had to do for AMSOL. Your job should now be submitted to the queue.
4) You may type qsr to see a list of all jobs running on the C-90. You should see yours. Once yours has disappeared from the list, it's done! These jobs take much longer than semiempirical jobs, so be patient.
5) You may now look at your ".out" file with less something.out. Type man less to get a help screen on less. If you do this while your job is running, type Shift-G to advance to the new end-of-file. The space bar will only advance you up to the place which was the end of the file when you started looking at it.
6) Several files may be deleted after your job has successfully completed. You may erase anything with ".run", ".e" and ".o" extensions (rm *.run, for example).
7) You should have a little less than 1 hour of cpu time left. This problem set will chew up most of what you have left. Type msiquery to see how many SUs you've used, and how many you have left.
8) YOU MAY RUN OUT OF TIME!!! I strongly recommend that you work one problem through to completion before you begin the next. If you do use up all of your SUs, you will not even be able to log in and look at your files, so write down the important information as your jobs finish.
9) If you have problems at any time, don't hesitate to ask for help. That's what Mike and I are here for.
10) Manuals may be found in the Kolthoff computer lab, and on-line at Gaussian.
The Questions (word-processed answers greatly preferred):
1) This problem explores free energies of reaction using the same molecules used for question 1 of the last problem set. Write G94-style z-matrices for H2, acetylene, ethylene and ethane (no benzene this time). We will use G2MP2 theory to study these. G2MP2 is a variation of G2 theory (presented in class) in which the higher-order corrections are carried out at the MP2 level of theory, rather than the MP4 level of theory. Consequently, it is much cheaper. The sole keyword you need is G2MP2 (but don't forget your %mem and %chk lines). This keyword launches a series of calculations.
Scan down to the bottom of your .out file (Shift-G gets you there fast in less). You should see a line that reads "G2MP2 Free Energy=". This energy is in hartrees, and contains thermal and entropic corrections valid for 298.15 K and 1 atm. Make a note of this energy for all four species, and compute the free energy of hydrogenation for H2 + C2H2 and H2 + C2H4.
Create a table simliar to Table 1.2 from the previous problem set. How well does G2MP2 theory compare to experiment?
NOTE: To convert your relative energies to kcal/mol, multiply hartrees by 627.51.
2) Computational chemistry is often applied to predict or explain observed reactivity. In this problem, we will explore electrophilic aromatic substitution using density functional theory (DFT).
Consider nitrobenzene, and aniline. Geometries obtained at the BPW91/ 6-31G* level are presented in the attached appendix. You will use these geometries to carry out single-point (i.e. no optimization) calculations at the BPW91 /3-21G level. The optimizations to obtain the geometries you have been provided required 42 and 31 minutes, respectively, for nitrobenzene and aniline. (FYI: Benzene takes only 6 minutes at the same level. What a difference symmetry makes!)
Keywords for this problem:
# BPW91 3-21G
Run your two single-point jobs. These would be designated BPW91/3-21G//BPW91/6-31G*.
Near the bottom of the population analysis section, you will see the line "Atomic charges with hydrogens summed into heavy atoms:". Make a note of these charges for nitrobenzene and aniline.
What is the total charge in the ring in each case? If you react these molecules with an electrophile, where would you expect the electrophile to attack? Which molecule should react faster, based on charges alone? Is this consistent with what you learned about electrophilic aromatic substitution in sophomore organic chemistry? Why or why not?
3) Another popular use for computational chemistry is in the prediction of relative energies of compounds, and their relative populations in a mixture.
Consider the case of acrolein:

Acrolein can adopt s-cis and s-trans conformations. Experimental data (microwave; Cherniak and Costain, J. Chem. Phys. 1966, 45, 104) suggest that the s-trans conformer is the sole detectable conformer. Assuming that the interconversion barrier is low (< 10 kcal/mol), isomerization should occur rapidly at room temperature (i.e. the rotation is under thermodynamic control). If this is the case, the equilibrium populations may be determined by:
a) Optimize structures for the s-cis and s-trans conformations of acrolein at the HF/cc-pVDZ level of theory. To save you time, reasonable starting geometries are provided in the appendix. All atoms are co-planar, so all dihedrals are either 0. or 180. degrees. Be sure to name a checkpoint file!
Keywords for part a):
# cc-pVDZ opt=z-matrix
b) To compute the free energy, we need to apply thermal and entropic corrections. These are easily obtained by running a frequency calculation. We will make use of the checkpoint file to give us the optimized geometry and wavefunction, which saves us and the computer a bit of time. Your entire input file for this job should look like:
%mem=6MW
%chk=s-cis.chk
# cc-pVDZ freq=noraman
geom=checkpoint
guess=read
frequency calculation on s-cis acrolein, optimized at HF/cc-pVDZ
0 1
(blank line terminates)
That's it. Do not include the molecule specification, or your job will crash. The GEOM=CHECKPOINT keyword tells G94 to pull the optimized geometry from the checkpoint file (s-cis.chk in this example), and GUESS=READ pulls the converged wavefunction from the same file.
These jobs are relatively long (ca. 5 minutes), so be patient. The NORAMAN modifier on the FREQ keyword supresses the calculation of the raman activities, which saves us about three minutes of cpu time.
Once your frequency has completed, scan through the .out file and confirm that your frequencies are all positive, and that your geometry is converged. Locate the line that reads "Sum of electronic and thermal Free Energies=". This energy contains thermal and entropic corrections appropriate for 298.15 K and 1 atm. Write this number down for both isomers, and compute DG for this isomerization in kcal/mol.
Using this number and the above equation, calculate the equilibrium composition of acrolein. Do your results agree with the experimental observation?
c) Look up the paper by Cherniak and Costain mentioned above. Locate the line in your frequency output that is labeled "Rotational constants (GHZ)". This comes directly below the "Standard Orientation" Cartesian coordinates. These are listed in the order A0, B0 then C0. Compare your computed rotational constants to the experimental values in the paper. Also compare your computed structure for the s-trans isomer to the experimentally determined structure. Are you satisfied with the agreement of your rotational constants and geometry with those of Cherniak and Costain? Why or why not?
Extra information
I have taken the liberty of computing the transition state for this process. If you have the time and inclination, you may wish to search for it yourself. I found the free energy of activation of be 7.9 kcal/mol for the s-trans - s-cis isomerization. Therefore, this process can be considered rapid and under thermodynamic control at standard temperature and pressure.
For Problem 2:
A resonable z-matrix would be a modification of the benzene z-matrix you used for Problem Set 2. You will need to reduce the symmetry, though. Aniline is Cs symmetric, with a pyramidal amine, and nitrobenzene is C2v symmetric, with all atoms co-planar. I used the following structure to build my z-matrices.
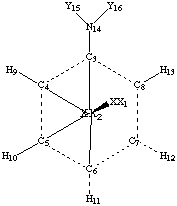
| BPW91/6-31G* geometries: | |||
| Aniline (Y=H) | Nitrobenzene (Y=O) | ||
| 2-3: | 1.4286 Å | 2-3 | 1.4071 Å |
| 2-4, 2-8: | 1.4067 Å | 2-4, 2-8: | 1.4229 Å |
| 2-5, 2-7: | 1.3933 Å | 2-5, 2-7: | 1.3896 Å |
| 2-6: | 1.4037 Å | 2-6: | 1.3779 Å |
| 2-9, 2-13: | 2.5019 Å | 2-9, 2-13: | 2.5132 Å |
| 2-10, 2-12: | 2.4876 Å | 2-10, 2-12: | 2.4826 Å |
| 2-11: | 2.4976 Å | 2-11: | 2.4712 Å |
| 2-14: | 2.8302 Å | 2-14 | 2.8886 Å |
| 14-15, 14-16: | 1.0186 Å | 14-15, 14-16: | 1.2424 Å |
| 3-14-15, 3-14-16: 114.8181o | 3-14-15, 3-14-16: 117.5492o | ||
| 3-1-2-4, -(3-1-2-8), 3-1-2-9, -(3-1-2-13): 59.8209o | 3-1-2-4, -(3-1-2-8), 3-1-2-9, -(3-1-2-13): 59.2766o | ||
| 3-1-2-5, -(3-1-2-7), 3-1-2-10, -(3-1-2-12): 119.7538o | 3-1-2-5, -(3-1-2-7), 3-1-2-10, -(3-1-2-12): 119.0512o | ||
| 4-3-14-15, 8-3-14-16: 24.5245o | |||
| 4-3-14-15, 8-3-14-16: fixed at 0o | |||
| 3-1-2-6, 3-1-2-11: fixed at 180o | 3-1-2-6, 3-1-2-11: fixed at 180o | ||
| 3-1-2-14: fixed at 0o | 3-1-2-14: fixed at 0o | ||
For Problem 3:
Recommended starting geometries for s-trans and s-cis acrolein:
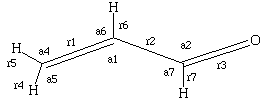
| s-trans | s-cis | ||
| r1 | 1.324 | 1.325 | |
| r2 | 1.480 | 1.488 | |
| r3 | 1.187 | 1.189 | |
| r4 | 1.082 | 1.083 | |
| r5 | 1.085 | 1.082 | |
| r6 | 1.083 | 1.084 | |
| r7 | 1.104 | 1.102 | |
| a1 | 121.3 | 121.4 | |
| a2 | 123.9 | 124.3 | |
| a3 | 122.0 | 121.7 | |
| a4 | 121.3 | 120.3 | |
| a5 | 122.4 | 121.5 | |
| a6 | 115.0 | 115.2 |
Remember, it's all co-planar (Cs symmetric).