1)

Table 1.1: Total G2MP2 free energies (hartrees).

H2	-1.177806
C2H2	-77.202980
C2H4	-78.435157
C2H6	-79.650372

Table 1.2: Comparison of computed (G2MP2) and experimental free energies of hydrogenation of acetylene and ethylene (kcal/mol).

	H2 + C2H2 --> C2H4	H2+ C2H4 --> C2H6
computed	-34.1	-23.4
experimental	-33.7	-24.1
error	-0.4 (-1.2%)	0.7 (2.9%)

For both reactions, G2MP2 theory agrees to within 1 kcal/mol of experiment. Clearly, the agreement for this level of theory is much better than what we achieved at the semiempirical level. However, the amount cpu time required is substantially greater. It would be challenging to perform G2MP2 calculations on systems much larger than 7 or 8 heavy atoms. Lower levels of ab initio theory may be comfortably performed on systems with 20 heavy atoms, while semiempirical theory is applicable on a routine basis to systems as large as 100 heavy atoms. It all comes back to a tradeoff between desired accuracy, and overall computational cost.

2)

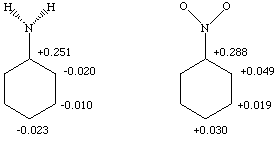
Your charge distribution should look something like the following. My geometry is the correct pyramidal one for aniline. If you used any other geometry, your charges may differ slightly.

The total charge in the aniline ring is +0.168 esu (-0.083 if we discount the carbon to which the substituent is attached), while it is considerably greater in the nitrobenzene ring at +0.454 esu (+0.166).

An electrophile will preferentially attack at locations of negative charge. In the case of aniline, the ortho and para positions show the greatest localization of negative charge. Furthermore, all three possible positions of attack (ortho, meta and para) bear negative charges, indicating that the amine group activates this ring towards attack by an electrophile.

For nitrobenzene, all positions in the ring are positive, indicating that the ring is deactivated towards electrophilic substitution in general. However, the meta position is much less positive than the ortho or para positions, so if an electrophile is going to attack, it would most likely do so at the meta position.

All of this is completely consistent with what we learned in undergraduate organic chemistry. An amine group activates an aromatic ring towards electrophilic substitution, and directs the electrophile to the ortho and para positions. A nitro group deactivates an aromatic ring towards electrophilic substitution, and directs the electrophile to the meta position. This problem shows very satisfying agreement between experiment and theory.

3) a)

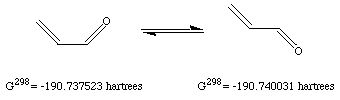
b) My results indicate that the s-trans isomer is 1.57 kcal/mol more stable than the s-cis isomer. Plugging this number into the free energy relationship, I calculate that the s-trans isomer will be favored by 14.2:1 over the s-cis isomer. This is equivalent to a equilibrium mixture that would be 93% s-trans and 7% s-cis.

If we are to believe this number and the experimental observation, then a 7% population is undetectable by microwave spectroscopy. I don't believe that microwave spectroscopy is that insensitive. Besides, there are a couple of potential problems with our computed results.

First, the HF/cc-pVDZ level of theory is probably not adequate to gauge reliably the energy difference between these two isomers. To check this, we would want to run single-point correlated calculations at successively higher levels of theory and larger basis sets until the energy gap converged. Also, our computed geometry may not be sufficient. Again, we should test convergence of the geometry against better calculations. As is often the case, the geometry will likely converge with respect to level of theory before the relative energies do.

There are also some questions which could be asked of the experimental results. More on this below.

c)

Table 3.1: Experimental and computed (HF/cc-pVDZ) rotational constants for s-trans acrolein, A₀, B₀, C₀. (GHz).

Experimental	Calculated	Error
47.3533	48.3483	0.995 (2.1%)
4.6594	4.7106	0.0512 (1.1%)
4.2428	4.2924	0.0496 (1.2%)

While the experimental and calculated values for A₀ differ by nearly 1 GHz, that difference amounts to only a 2.1% error. Since rotational constants are very sensitive to the geometry, even slight differences in the experimental and computed geometries will show themselves in the rotational constants. In general, while the agreement could be better, I find it to be satisfying.

The following figure shows the computed structure for s-trans acrolein, with the experimental numbers in parenthesis.

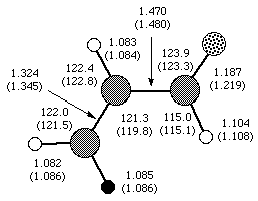
While generally good agreement is seen for the C-H bond lengths, and the majority of the bond angles, fairly poor agreement is seen for the C-C and C-O bond lengths. We can expect theory to be good at least to 0.001 Å and 0.1°. Both experiment and theory may be at fault here. The authors point out a number of assumptions which were made and discrepancies among the experimental data. It is possible that modern techniques would yield a more highly refined structure with smaller error bars. It is also highly likely that our computed geometry can be improved by moving to a higher level of theory and a bigger basis set.

Overall, the level of theory used for this problem has given us qualitative agreement with experiment. Our results show the correct trend, without giving perfect agreement with experiment. This is very common in computational studies. Given more resources, the computational result can be improved. Nevertheless, the results are satisfying for the HF level of theory.