A practical reminder: To run a job, you're input file should be called myfile.dat. Simply issue the command qrun myfile.dat and the script will take care of the rest. If you want to look at an output deck while a job is running, you can either vi myfile.out or more myfile.out. To examine the load leveler queue on the sp, the command is llq.

A nomenclature reminder: the notation x/y//w/z means level of theory x using basis set y at a geometry optimized at level of theory w with basis set z. E.g., MP4/6-311G**//HF/6-31G* means the geometry was optimized at the HF/6-31G* level but the energy (and/or other properties) are being calculated at the MP4/6-311G** level.

Some quick notes/reminders with respect to Gaussian94:

1) Always include the keyword: scf=direct.

2) Always specify freq=noraman for frequency calculations.

3) To find transition states in the absence of a symmetry constraint, use fopt=(ts).

4) You can save a lot of time by using useful information from previous calculations stored in the checkpoint file. Plan your calculations to try to save time.

a) Keywords guess=read and geom=checkpoint get the wave function and the geometry, respectively, from the last completed calculation. So, if you have just done an optimization, and want to follow-up with a frequency calculation, you will certainly want to use these keywords. Note: Frequencies must be calculated using the same level of theory with which the geometry was optimized!

b) If you just optimized a geometry at one level of theory, and want to repeat that optimization at a different level, include readfc in the fopt=() keyword, e.g., fopt=(ts,readfc). This causes the program to start with the force constants from the previous calculation, which is efficient. It's usually a good idea to work your way up in a geometry optimization so you don't waste a lot of computer time because of a bad initial guess.

The Problems:

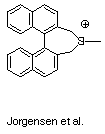
1. Last problem set, we examined the claims of Jorgensen et al. to have synthesized an isolated silicenium ion. More accurately, we showed why even arylsilicenium ions are highly unstable, raising doubts that an alkyl silicenium ion would be isolable. Let's now put the nails in the coffin. First, optimize the structure of tetramethylsilane (TMS) at the HF/STO-3G* level. Now, compute the NMR shielding of 29Si in TMS at the HF/3­21G*//HF/STO-3G* level (the keyword required is nmr). What is the absolute isotropic shielding in ppm? Now, compute the isotropic shielding of 29Si in PhSiH2+ at the HF/3­21G*//HF/STO-3G* level. Relative to TMS (which is the compound defining zero on the d scale for 29Si NMR) what is d for 29Si in PhSiH2+ (remember that d is relative de shielding)? Jorgensen et al. report a d value of 34 ppm for 29Si in their cation-does this seem possible given your calculations so far? Jorgensen et al. performed their experiments in acetonitrile (CH3CN). Compute the 29Si NMR d value for PhSiH2+ CH3CN. Is your value closer to that reported for the experimental system? Look at your structure for PhSiH2+ CH3CN; does it seem to be a true silicenium ion? Why or why not? If not, where is the positive charge localized? Should the Jorgensen et al. paper have been published?

2. We now return to the anomeric rotational potential studied in both prior Problem Sets, where MMX and PM3 gave inconsistent results. For the case of 2-methoxy-1,3-tetrahydropyran, find at least one minimum energy structure and one transition state structure at the RHF/3-21G level-provide pictures of your structures. Verify the nature of these structures with frequency calculations. What is the magnitude of the imaginary frequency for your TS structure? Compute single-point energies at the B3LYP/6­31G*//HF/3-21G level (use scf=(tight,direct) in single-point keywords). What is your calculated rotational potential barrier? Based on your ab initio calculations, was MMX or PM3 more accurate for this molecule? Explain your answer.

3. Using your results from the above Problem 2, and assuming that your minimum and barrier are unique on the torsional potential energy surface, what does transition state theory predict the rate constant for rotation to be at 298 K? (Recall TST says that the rate constant for this unimolecular process is kBT/h x exp(-DG‡/RT) where kB is Boltzmann's constant, h is Planck's constant, R is the universal gas constant, T is temperature, and DG‡ is the free energy of activation). To compute the free energies of your species, use your B3LYP/6­31G*//HF/3-21G energies for potential energy, and add the free energy contributions determined by your frequency calculations at the HF/3-21G level. Now, compute the aqueous solvation free energies for your two structures at the SM5.42R/AM1 level using AMSOL (the keywords will be AM1 SM5.42R 1SCF SOLVNT=WATER TRUES HFCALC=1SCF). By what factor is solvation predicted to affect the rotational rate constant (i.e., how does the rate change when you modify DG‡(gas) to instead be DG‡(aqueous)?)