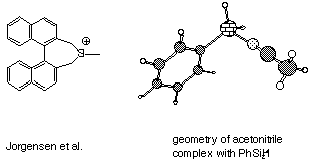
1. Last problem set, we examined the claims of Jorgensen et al. to have synthesized an isolated silicenium ion. More accurately, we showed why even arylsilicenium ions are highly unstable, raising doubts that an alkyl silicenium ion would be isolable. Let's now put the nails in the coffin. First, optimize the structure of tetramethylsilane (TMS) at the HF/STO-3G* level. Now, compute the NMR shielding of 29Si in TMS at the HF/3­21G*//HF/STO-3G* level (the keyword required is nmr). What is the absolute isotropic shielding in ppm? Now, compute the isotropic shielding of 29Si in PhSiH2+ at the HF/3­21G*//HF/STO-3G* level. Relative to TMS (which is the compound defining zero on the d scale for 29Si NMR) what is d for 29Si in PhSiH2+ (remember that d is relative de shielding)? Jorgensen et al. report a d value of 34 ppm for 29Si in their cation-does this seem possible given your calculations so far? Jorgensen et al. performed their experiments in acetonitrile (CH3CN). Compute the 29Si NMR d value for PhSiH2+ CH3CN. Is your value closer to that reported for the experimental system? Look at your structure for PhSiH2+ CH3CN; does it seem to be a true silicenium ion? Why or why not? If not, where is the positive charge localized? Should the Jorgensen et al. paper have been published?

The absolute shielding of TMS (isotropic) is computed to be 514.2 ppm at the indicated level. At the same level, the d values for PhSiH2+ and PhSiH2+ CH3CN are computed to be 218.4 and 12.1 ppm, respectively. Only the latter is anywhere remotely close to the experimentally reported value (the remaining discrepancy is not unreasonable given the structural differences between our simple aryl system and the real system-calculations on the real molecule at a higher level of theory (too expensive for classwork) give much better agreement). The acetonitrile complex has a normal, covalent Si-N bond length. That is, there is zero silicenium ion character. Instead, the cationic character is at the nitrile carbon (the atomic partial charges bear this out as well). Indeed, one might best view this as a methylated silyl isonitrile. Clearly, the referees on the Jorgensen paper failed rather badly. Work by Olah et al. is currently in press at JACS pointing out these serious errors.

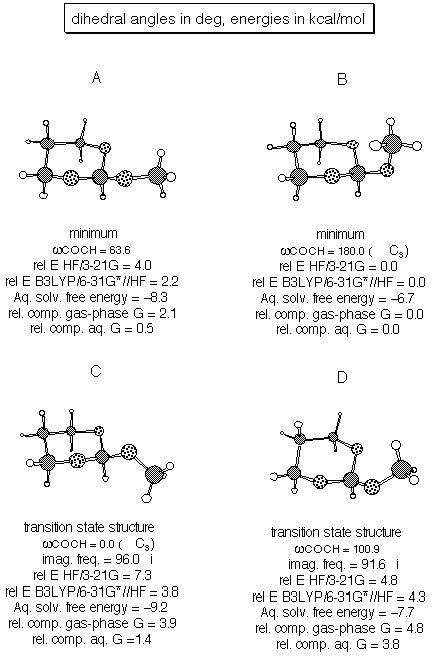
2. We now return to the anomeric rotational potential studied in both prior Problem Sets, where MMX and PM3 gave inconsistent results. For the case of 2-methoxy-1,3-tetrahydropyran, find at least one minimum energy structure and one transition state structure at the RHF/3-21G level-provide pictures of your structures. Verify the nature of these structures with frequency calculations. What is the magnitude of the imaginary frequency for your TS structure? Compute single-point energies at the B3LYP/6­31G*//HF/3-21G level (use scf=(tight,direct) in single-point keywords). What is your calculated rotational potential barrier? Based on your ab initio calculations, was MMX or PM3 more accurate for this molecule? Explain your answer.

Figures on the next two pages provide the critical data for this problem. Note how poorly RHF/3-21G does for relative energies compared to B3LYP/6-31G*. Note also how sensitive the aqueous solvation free energy is to conformation (the best solvated conformer is C, with all oxygen lone pairs pointing in the same direction for optimal solvation).

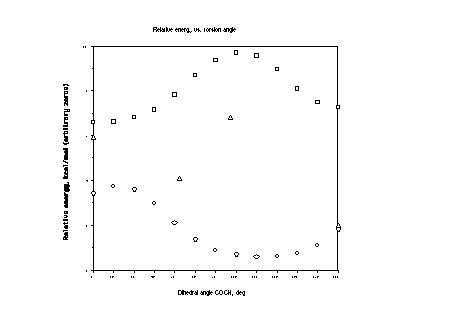
Above is the curve of relative energies, where squares are PM3 and circles MMX and triangles B3LYP/6-31G*//HF/3-21G. I haven't bothered to smooth the DFT curve. As to which level of theory is better, MMX of PM3, the answer is somewhat depressing. Neither does a great job, but PM3 is better. MMX has a minimum at zero, where a local maximum on the coordinate should be, a maximum at 180, where a minimum should be, and completely misses the barrier at 105 deg. PM3 properly has a minimum at 180, but fails to recognize it as the global minimum. Also, PM3 has the secondary minimum in the wrong place. In essence, PM3 fails to appreciate the full magnitude of the anomeric effect, which should increasingly pull the energy down as one travels from 0 to 180-or, in other words, if we were to add a line of negative slope to the PM3 curve it would reproduce the DFT curve reasonably well. So, the anomeric effect is hard. Too bad, since we had such a nice rationalization of our results for Problem Set 1 in terms of the anomeric effect. This illustrates a general rule of theory: you can rationalize anything, but you might want to avoid it until you're sure you're prediction is correct!

3. Using your results from the above Problem 2, and assuming that your minimum and barrier are unique on the torsional potential energy surface, what does transition state theory predict the rate constant for rotation to be at 298 K? (Recall TST says that the rate constant for this unimolecular process is kBT/h x exp(-DG‡/RT) where kB is Boltzmann's constant, h is Planck's constant, R is the universal gas constant, T is temperature, and DG‡ is the free energy of activation). To compute the free energies of your species, use your B3LYP/6­31G*//HF/3-21G energies for potential energy, and add the free energy contributions determined by your frequency calculations at the HF/3-21G level. Now, compute the aqueous solvation free energies for your two structures at the SM5.42R/AM1 level using AMSOL (the keywords will be AM1 SM5.42R 1SCF SOLVNT=WATER TRUES HFCALC=1SCF). By what factor is solvation predicted to affect the rotational rate constant (i.e., how does the rate change when you modify DG‡(gas) to instead be DG‡(aqueous)?)

The following data answer this question, which depends on which minimum and which TS structure you found. Refer to pictures in answer 2 for structures. Note how large an effect solvation can have on the rate constant for even a fairly simple process like bond rotation.

Minimum/TS Pair	k(gas)	k(aq)	Effect of aqueous solvation
A --> C	3.2x1011	1.4x1012	4.4-fold acceleration
A --> D	6.8x1010	2.6x1010	2.6-fold deceleration
B --> C	9.3x109	6.1x1011	65-fold acceleration(!)
B --> D	1.9x109	1.1x1010	5.7-fold acceleration