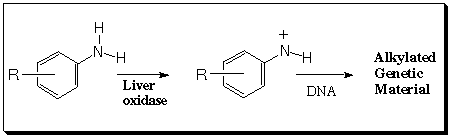
Abstract: Aromatic nitrenium ions have been postulated as carcinogenic species derived from the in vivo catabolism of aromatic amines. Nitrenium ions incorporate a disubstituted, positively charged nitrogen atom, and may thus have either singlet or triplet spin multiplicity. The former spin state is implicated in carcinogenesis. We have calculated singlet-triplet gaps for a number of small to medium-sized nitrenium ions, in particular nitrenium, imenium, methylnitrenium, aziridenium, and phenylnitrenium; similar calculations have also been done for the analogous isoelectronic carbenes and for other valence isoelectronic analogs in the XH2 series. Several levels of theory have been employed, including multi-configuration self consistent field, multi-reference configuration interaction, coupled-cluster theory, and density functional theory. The electronic and steric factors that influence the singlet-triplet gaps for these species are discussed, and the levels of theory are compared. Density functional theory appears to hold promise for larger, biologically relevant nitrenium ions.
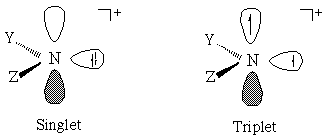
We have been intrigued by the possibility that density functional theory (DFT) might be particularly suited to overcome some of these challenges. DFT includes correlation within an SCF formalism and additionally has the desirable properties that in its spin-polarized form it generally suffers minimally from spin contamination.[15,16] And, of course, it is extremely rapid by comparison to multiconfigurational techniques.[17,18] DFT is not in general applicable to molecular excited states, but has been shown to be formally applicable to the lowest energy electronic state for each symmetry irreducible representation for a given system.[19-21] There is thus no ambiguity in calculating S-T gaps for systems in which the ground state symmetries for the two multiplicities are disparate, like those considered here.
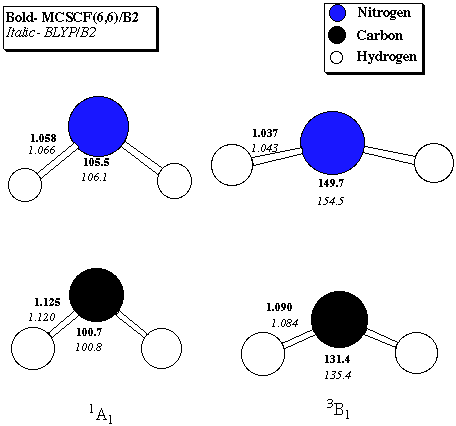
Table 1. 1A1 - 3B1 Singlet-Triplet gaps (kcal/mol) for nitrenium ion and methylene Level of Theory Nitrenium Methylene MCSCF(6,6)/B1 29.7 11.9 MRCISD/B1//MCSCF(6,6)/B1 32.0 11.5 MCSCF(6,6)/B2 29.2 11.3 MRCISD(Q)/B1//MCSCF(6,6)/B2 30.5 10.0 BVWN5/B1 29.5 9.8 BLYP/B1 31.2 10.5 BVWN5/B2 29.3 9.6 BLYP/B2 30.6 10.0B1 = correlation-consistent polarized valence-double-zeta (Dunning)
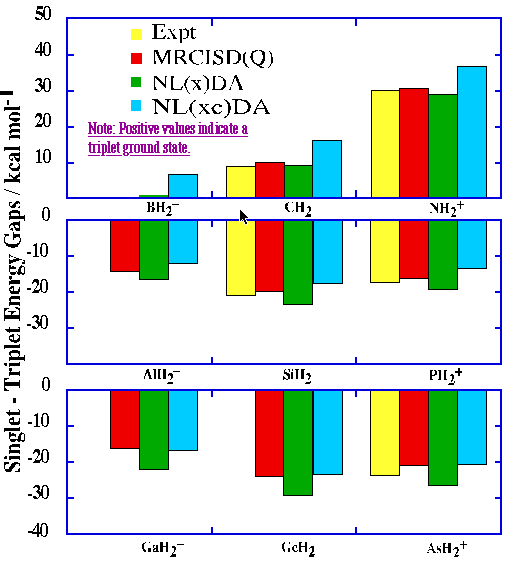
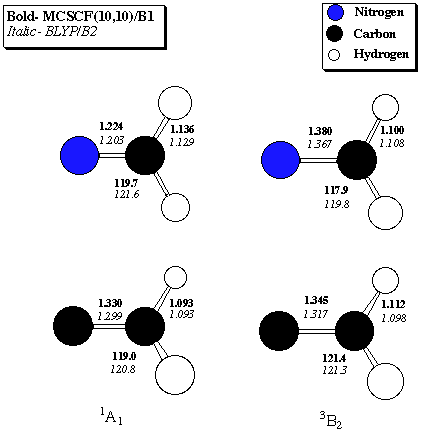
Table 2. 1A1 - 3B2 Singlet-Triplet gaps (kcal/mol) for imenium ion and vinylidene Level of Theory Imenium Vinylidene CCSD(T)/B1 -58.4 -44.3 MCSCF(10,10)/B1 -54.7 -38.0 BVWN5/B2 -61.5 -47.9 BLYP/B2 -61.5 -48.3 BVWN5/B2//MCSCF(10,10)/B1 -61.1 -47.6 BLYP/B2//MCSCF(10,10)/B1 -61.2 -48.0 BVWN5/B3//MCSCF(10,10)/B1 -61.2 -48.0 BLYP/B3//MCSCF(10,10)/B1 -61.3 -48.3B1 = correlation-consistent polarized valence-double-zeta (Dunning)
The high energies of the triplet states may give rise to the larger discrepancies observed for these cases between CCSD(T), MCSCF, and DFT. The DFT gaps are relatively insensitive to the theoretical level at which the geometries were optimized. They also appear to be well converged with respect to basis set. The CCSD(T) gaps are about 3 kcal/mol smaller, and the MCSCF numbers are roughly that much smaller again. In this instance, the MCSCF calculations are full valence complete active space, so it seems unlikely that multirefrence configuration interaction would account for the 6 to 7 kcal/mol difference between MCSCF and DFT. Another possibility is that the MCSCF and DFT numbers would agree more closely were the MCSCF calculations to be carried out at the valence-triple-zeta level. The observed quantitative discrepancies for such a large gap are probably of minimal import.
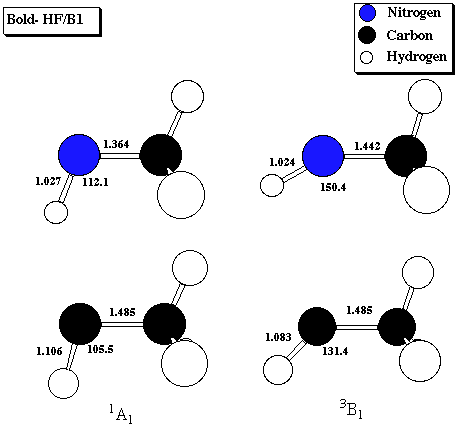
Table 3. 1A1 - 3B1 Singlet-Triplet gaps (kcal/mol) for
methylnitrenium ion and ethylidene
Level of Theory Methylitrenium Ethylidene
CCSD(T)/B1//HF/B1 13.2 7.3
MCSCF(6,6)/B1//HF/B1 14.9 8.0
BVWN5/B2//HF/B1 6.8 4.3
BLYP/B2//HF/B1 6.9 4.2
BVWN5/B3//HF/B1 6.9 4.1
BLYP/B3//HF/B1 6.8 3.9
B1 = correlation-consistent polarized valence-double-zeta (Dunning)
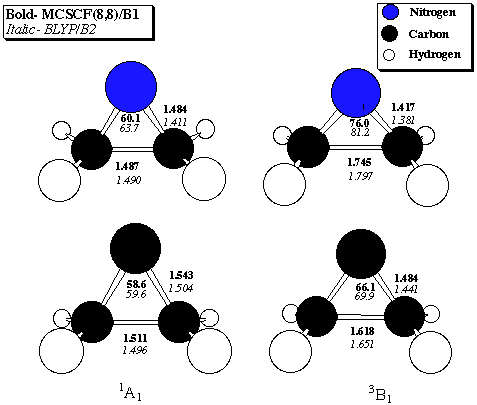
Table 4. 1A1 - 3B1 Singlet-Triplet gaps (kcal/mol) for aziridenium ion
and cyclopropylidene
Level of Theory Aziridenium Cyclopropylidene
CCSD(T)/B1//MP2/B1 10.8 -13.3
MCSCF(8,8)/B1 11.4 -13.0
BVWN5/B2 9.4 -13.1
BLYP/B2 8.4 -12.9
MCSCF(8,8)/B2//MCSCF(8,8)/B1 10.4 -14.1
BVWN5/B2//MCSCF(8,8)/B1 11.0 -13.6
BLYP/B2//MCSCF(8,8)/B1 10.7 -13.5
BVWN5/B3//MCSCF(8,8)/B1 11.1 -13.7
BLYP/B3//MCSCF(8,8)/B1 10.8 -13.6
B1 = correlation-consistent polarized valence-double-zeta (Dunning)
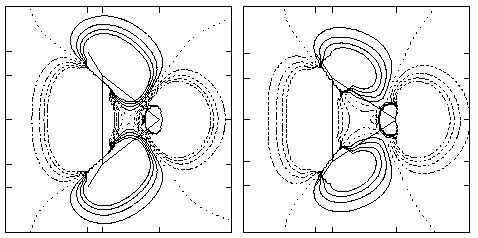
Density Plot: The density difference map for the 1A1 and 3B1 states (0.01 au contour intervals, dashed lines are negative, solid lines are positive) obtained by subtraction of the former from the latter for aziridenium (left) and cyclopropylidene (right) taken in the plane of the three membered ring. The hypovalent atom is at the right in each case.
These long bonds are explained beginning with analysis of the electronic structures of the singlets. Most carbene and nitrenium ion singlets are typically regarded as having a dominant configuration where the highest occupied molecular orbital (HOMO) corresponds to a lone-pair-like orbital in the plane of the substituents; the perpendicular p orbital lies empty. In these molecules, however, the "back" of the lone pair orbital has considerable overlap with the bonding orbital connecting the two methylene groups at the base of the three-membered ring. Hybridization thus occurs to create a HOMO with considerable amplitude in the C-C bonding region. Hybridization occurs to a larger degree for the nitrenium cation because of its lower energy lone pair. Since formation of the triplet involves promotion of one electron from the HOMO to the lowest unoccupied molecular orbital (LUMO), some C-C bonding density is removed. Mulliken population analysis of aziridenium at the MCSCF level supports this view; a shift in charge of 0.17 electrons from the two methylene groups to the nitrogen atom occurs on going from the singlet to the triplet. The above density plot illustrates this point with a physical observable, namely density difference maps in the planes of the rings. Both maps illustrate a loss of density from the C-C bonding region.
Energies: CCSD(T), MCSCF, and DFT calculations all agree quite well for both these systems. S-T gaps calculated at the DFT level are sensitive to molecular geometry. There are insufficient experimental data to judge whether DFT or MCSCF (or MP2) geometries are more accurate. The DFT predicted S-T gaps are apparently well converged with respect to basis set. The gap for cyclopropylidene is in good accord with that predicted by Honjou et al. at the SDQCI/DZP//HF/DZP level, -12.4 kcal/mol.[26]
Finally, placing the isoelectronic carbene or nitrenium centers in a 3-membered ring has similar effects on the calculated S-T gaps relative to the parent XH2 systems. Relative to CH2 and NH2+, with experimentally determined S-T gaps of 9.00 +/- 0.01[27] and 30.1 +/- 0.2[28] kcal/mol, respectively, in each case the singlet is stabilized by roughly 20 kcal/mol. Most of this stabilization probably arises from the small bond angles enforced by the ring at the divalent center. Disubstituted carbene and nitrenium triplets generally have much wider bond angles than their respective singlets since they allocate more s character to their bonding orbitals. As shown in the density difference maps, the deficiency of bonding density in the region between the two methylene groups coincides with the triplets being able to open to the calculated MCSCF bond angles at the hypovalent centers.[29]
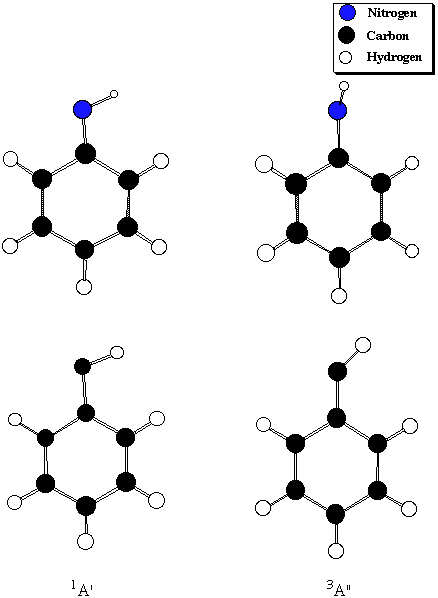
Table 5. 1A' - 3A" Singlet-Triplet gaps (kcal/mol) for phenylnitrenium
and phenylcarbene
Level of Theory Phenylnitrenium Phenylcarbene
PMP4/B1 -26.8 2.4
BVWN5/B2 -21.2 4.3
(Expt. XH2) 30.1 9.0
(Effects of Ph substitution) -51.3 -4.7
The results underline the dissimilarities found in these isoelectronic systems.
MCSCF calculations were prohibitively expensive for the size of the active space deemed necessary to fully describe the systems.
In particular, orbitals with significant contributions from the
nitrogen in phenylnitrenium were low enough in energy to interact with
the sigma framework.
DFT generally has much lower levels of spin contamination in open
shell systems relative to UHF.
The large singlet stabilization by phenyl substitution for nitrenium derives
from the considerably enhanced pi-acceptor characteristics of a positively
charged nitrogen compared to a neutral carbon--this differential
pi-accepting ability is more manifest in the singlets, where an empty p
orbital serves as acceptor, than it is in the triplets. Singlet stabilization
for the weakly electron-deficient carbene is by comparison smaller in
magnitude[13]--one measure of this is that while singlet
phenylnitrenium prefers to isomerize by inverting (like an imine), singlet
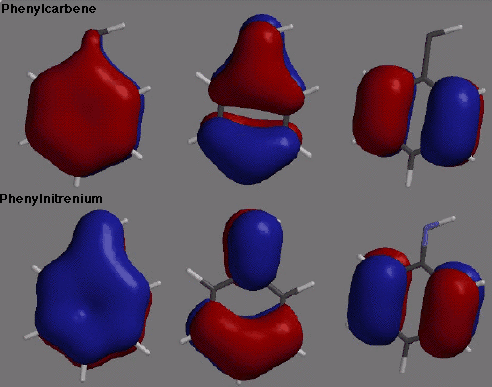
phenylcarbene breaks pi conjugation by rotating out of plane. The orbitals displayed
in the picture accompanying the title illustrate these points exactly. In particular, the
coefficient of the p orbital on the nitrenium nitrogen is quite large for the lowest
energy pi orbital of phenylnitrenium. In phenylcarbene, on the other hand, there is very
little contribution from the carbene p orbital to this MO. The next higher energy MO is
similarly differentiated.
The singlet is the lower energy spin state for phenylnitrenium. However,
substitution of the aromatic ring with pi-acids and/or sigma-donors can
decreases the gap between the pi LUMO and the sigma HOMO, and can
thereby make the triplet spin state accessible.[16,31,32,33,34] DFT should be a promising method for modeling
this effect.
Geometry optimizations were also carried out using spin-polarized density
functional theory (DFT) with both local and gradient-corrected functionals.
Several combinations of functionals were employed. BVWN5 combines Becke's
non-local exchange functional[41] with a local correlation
functional of Vosko, Wilks, and Nusair.[42] BLYP, replaces
the correlation functional with a local/non-local alternative developed by Lee,
Yang, and Parr.[43] In the XH2 series, BP replaces the
correlation functional with a non-local alternative developed by Perdew.[44]
Carbene and nitrenium ion optimizations at the DFT level were carried out using
the B1 and B2 basis sets. However, for the isoelectronic XH2 series, DFT
calculations employed the uncontracted Slater-type-orbital triple-zeta basis
sets of Snijders et al.[45] with one p and one d function added to hydrogen
and one d and one f function added to the heavy atoms. Effective core
potentials for the third row atoms were used only for the innermost 18
electrons; 28-electron core potentials (i.e., including the 3d block)
correlated about 1 kcal/mol less well with the MRCI results. Auxiliary s, p, d,
f, and g functions were used for all nuclei to fit the molecular density during
the SCF procedure. These levels of theory, with and without the Perdew
non-local correction, respectively, are referred to as NL(x)DA/TZ2P and NL(xc)DA/TZ2P in the
figure above.
Stationary points were characterized by analytic frequency calculations where
appropriate.
Spin contamination ranged from slight to severe in UHF triplet calculations.
The worst case was phenylcarbene, for which
Single point calculations were performed at various geometries using both
larger basis sets (for DFT up to the valence quadruple-zeta cc-pVQZ[37] basis set with g functions removed, hereafter B3) and
selected post-HF levels of theory. In particular, coupled-cluster calculations
including all single, double, and perturbative triple excitations (CCSD(T))[46-49] out of the HF reference configuration were performed.
Spin-projected fourth-order perturbation theory (PMP4) was also employed in the
phenylnitrenium/phenylcarbene case. Finally, in some cases single point
multireference configuration interaction calculations were performed
considering all single and double excitations from the CASSCF reference space
(core orbitals were frozen) into the space of all virtual orbitals (MRCISD).
Corrections for quadruple excitations were sometimes estimated using the
multireference analog of the Langhoff-Davidson correction [50] suggested by
Bruna et al. [51]. This level of theory is referred to as MRCISD(Q).
HF, MCSCF, and MRCI calculations were carried out using the GAMESS program
suite; [52] HF, MP2, CCSD(T), and DFT calculations were
carried out using the GAUSSIAN 92/DFT program suite.[53]
Some DFT calculations employed the Amsterdam Density Functional Program.[54]
(2) Scribner, J. D.; Naimy, N. Cancer Res. 1975, 35,
1416.
(3) Miller, E. C. Cancer Res. 1978, 27, 973.
(4) Singer, B.; Kusmierek, J. T. Annu. Rev. Biochem. 1982,
52, 655.
(5) Garner, R. C.; Martin, C. N.; Clayson, D. B. In Chemical
Carcinogens; 2 ed.; C. E. Searle, Ed.; American Chemical Society:
Washington, DC, 1984; Vol. 1.
(6) Abramovitch, R. A.; Jeyaraman, R. In Azides and Nitrenes: Reactivity
and Utility; E. F. V. Scriven, Ed.; Academic: New York, 1984.
(7) Stadler, W. M. Int. J. Oncol. 1993, 3, 549.
(8) Novak, M.; Kahley, M. J.; Eiger, E.; Helmick, J. S.; Peters, H. E. J.
Am. Chem. Soc. 1993, 115, 9453.
(9) Swaminathan, S.; Frederickson, S. M.; Hatcher, J. F. Carcinogenesis
1994, 15, 611.
(10) Panda, M.; Novak, M.; Magonski, J. J. Am. Chem. Soc. 1989,
111, 4524.
(11) Davidse, P. A.; Kahley, M. J.; McClelland, R. A.; Novak, M. J. Am.
Chem. Soc. 1994, 116, 4513.
(12) McClelland, R. A.; Davidse, P. A.; Hadzialic, G. preprint.
(13) Davidson, E. R. In Diradicals;W. T. Borden, Ed.; Wiley-Interscience:
New York, 1982; p. 73.
(14) Schaefer, H. F., III Science 1986, 231, 1100.
(15) Baker, J.; Scheiner, A.; Andzelm, J. Chem. Phys. Lett. 1993,
216, 380.
(16) Cramer, C. J.; Dulles, F. J.; Falvey, D. E. J. Am. Chem. Soc.
1994, 116, 9787.
(17) Ziegler, T. Chem. Rev. 1991, 91, 651.
(18) Density Functional Methods in Chemistry; Labanowski, J., Andzelm,
J., Eds.; Springer-Verlag: New York, 1991.
(19) Gunnarsson, O.; Lundqvist, B. I. Phys. Rev. B 1976,
13, 4274.
(20) Ziegler, T.; Rauk, A.; Baerends, E. J. Theor. Chim. Acta
1977, 43, 261.
(21) Jones, R. O.; Gunnarsson, O. Rev. Mod. Phys. 1989,
61, 689.
(22) Cramer, C. J.; Dulles, F. J.; Storer, J. W.; Worthington, S. E. Chem.
Phys. Lett. 1994, 218, 387.
(23) Ford, G. P.; Herman, P. S. J. Am. Chem. Soc. 1989,
111, 3987.
(24) Khodabandeh, S.; Carter, E. A. J. Phys. Chem. 1993,
97, 4360.
(25) Modarelli, D. A.; Platz, M. S. J. Am. Chem. Soc. 1993,
115, 470.
(26) Honjou, N.; Pacansky, J.; Yoshimine, M. J. Am. Chem. Soc.
1985, 107, 5332.
(27) Jensen, P.; Bunker, P. R. J. Chem. Phys. 1988, 89,
1327.
(28) Gibson, S. T.; Greene, P. J.; Berkowitz, J.; J. Chem. Phys.
1985, 83, 4319.
(29) Cramer, C.J.; Worthington, S.E.; J. Phys. Chem.
1995, 99, 1462.
(30) Glover,S.A.; Scott, A. P.; Tetrahedron
1989, 45, 1763.
(31) Karaman, R; Huang, J.-T. L.; Fry, J. L.; J. Comput. Chem
1991, 12, 536.
(32) Ford, G. P.; Scribner, J. D.; J. Am. Chem. Soc.
1981, 103, 4281.
(33) Falvey, D. E.; Cramer, C. J.; Tetrahedron Lett.
1992, 33, 1705.
(34) Li, Y.-Z.; Schuster, G. B.; J. Org. Chem.
1988, 53, 1273.
(35) (a) Roos, B. O.; Taylor, P. R.; Siegbahn, P. E. M. Chem. Phys.
1980, 48, 157. (b) Review: Roos, B. O. In Ab Initio
Methods in Quantum Chemistry; Vol. 2, Lawley, K. P., Ed., Wiley: New York,
1987, p. 399.
(36) Pulay, P.; Hamilton, T. P. J. Chem. Phys. 1988, 88,
4926.
(37) Dunning, T. H. J. Chem. Phys. 1989, 90, 1007.
(38) Stevens, W. J.; Krauss, M.; Basch, H.; Jasien, P. G.; Can. J. Chem.
1992 70, 612.
(39) Frisch, M. J.; Pople, J. A.; Binkley, J. S.; J. Chem. Phys. 1984
80, 3265.
(40) Hehre, W. J.; R. Ditchfield, R.; Pople, J. A.; J. Chem. Phys. 1972
56, 2257.
(41) Becke, A. D. Phys. Rev. A 1988, 38, 3098.
(42) Vosko, S. H.; Wilks, L.; Nussair, M. Can. J. Phys. 1980,
58, 1200.
(43) Lee, C.; Yang, W.; Parr, R. G. Phys. Rev. B 1988, 37,
785.
(44) Perdew, J. P.; Phys. Rev. B 1986 33, 8822.
(45) Snijders, G. J.; Baerends, E. J.; Vernooijs, P.; Atom. Data and Nucl. Data
Tabl. 26 1982, 483.
(46) Cizek, J. Adv. Chem. Phys. 1969, 14, 35.
(47) Purvis, G. D.; Bartlett, R. J. Chem. Phys. 1982, 76,
1910.
(48) Scuseria, G. E.; Schaefer, H. F., III J. Chem. Phys. 1989,
90, 3700.
(49) Raghavachari, K.; Trucks, G. W.; Pople, J. A.; Head-Gordon, M. Chem.
Phys. Lett. 1989, 157, 479.
(50) Langhoff, S. R.; Davidson, E. R.; Intern. J. Quantum Chem. 1973 7, 999.
(51) Bruna, P. J.; Peyerimhoff, S. D.; Buenker, R. J.; Chem. Phys. Letters
1980 72, 278.
(52) Schmidt, M. W.; Baldridge, K. K.; Boatz, J. A.; Elbert, S. T.; Gordon, M.
S.; Jensen, J. H.; Koseki, S.; Matsunaga, N.; Nguyen, K. A.; Su, S.; Windus, T.
L.; Dupuis, M.; Montgomery, J. A. J. Comp. Chem. 1993, 14,
1347.
(53) Frisch, M. J.; Trucks, G. W.; Schlegel, H. B.; Gill, P. M. W.; Johnson, B.
G.; Wong, M. W.; Foresman, J. B.; Robb, M. A.; Head-Gordon, M.; Replogle, E.
S.; Gomperts, R.; Andres, J. L.; Raghavachari, K.; Binkley, J. S.; Gonzalez,
C.; Martin, R. L.; Fox, D. J.; Defrees, D. J.; Baker, J.; Stewart, J. J. P.;
Pople, J. A. Gaussian 92/DFT, Revision G.1; Gaussian, Inc.: Pittsburgh,
PA, 1993.
(54) ADF, Version 1.0 (Department of Theoretical Chemistry, Vrije Universiteit,
Amsterdam, 1993).
Expanded Summary:
Calculations at the BVWN5/B2//BVWN5/B1 level of theory (294 basis functions)
were carried out for these two aromatic systems.[16] Key results are (i) the predicted S-T gaps (including
zero-point corrections) are -21.2 and 4.3 kcal/mol for phenylnitrenium ion and
phenylcarbene, respectively. (ii) Triplet phenylcarbene is a planar species and
has a predicted barrier to rotation about the exocyclic bond of 2.7 kcal/mol; the planar phenylnitrenium triplet, on the other
hand, is a rotational transition state (TS) structure. The local minimum has
instead the N-H bond perpendicular to the aromatic ring with a
rotational barrier of 1.8 kcal/mol. Although the DFT Hessian for the
planar phenylnitrenium structure has one negative force constant, high spin
contamination[30] causes the UHF Hessian matrix to have
none, a qualitatively incorrect result. (iii) Singlet phenylcarbene is a planar
species with a predicted barrier to rotation about the exocyclic bond of 11.0
kcal/mol--singlet phenylnitrenium does not rotate about this bond, but instead
inverts through nitrogen with a barrier of 26.0 kcal/mol.
Conclusions
Theoretical
Specific molecules
Greater orbital contraction at the cationic hypovalent center
increases triplet stabilization compared to uncharged or anionic centers. The increased s-character of sigma-orbitals at sp hypovalent
centers increases singlet stability; this effect is
larger for the nitrenium ions than for carbenes. Changes in the S-T gap arising from placing isoelectronic hypovalent centers
into 3-membered rings are energetically similar (about 20 kcal/mol
differential destabilization of the triplet)--there is less energetic similarity between carbenes and nitrenium ions in
other substituted systems. Unusually long bonds between the two methylene groups in the
3-membered rings are attributed to cationic one-electron bonds. Hyperconjugative stabilization of singlets is much more important for
(cationic) nitrenium ions than for carbenes; this is dramatically
illustrated in the case of phenyl substitution.
Back to contents
Implications for modeling aromatic amine
carcinogenesis:
Methods
We follow throughout the standard convention that x/y//z/w denotes a
calculation with method x and basis y at a geometry optimized
with method z and basis set w. Singlet and triplet carbenes and
nitrenium ions were optimized at a variety of theoretical levels, employing
Hartree-Fock (HF, restricted for singlets, unrestricted for triplets),
second-order perturbation theory (MP2), and multiconfiguration
self-consistent-field (MCSCF) techniques. MCSCF active spaces were constructed
from the two "lone-pair" orbitals on the hypovalent atoms and the
heavy-atom-heavy-atom bonding/antibonding orbitals. When practical, the active
space was expanded to include the entire valence space. All MCSCF calculations
are of the complete active space (CAS) variety.[35,36]
Employed basis sets include the correlation-consistent polarized valence
double-zeta (cc-pVDZ, hereafter referred to as basis set B1) and the
correlation-consistent polarized valence triple-zeta (cc-pVTZ, hereafter B2) basis sets
of Dunning and Woon [37]. For Ga, Ge, and As, the
relativistic effective core potential basis of Stevens et al.[38] was used
with either 10-electron (Ga) or 28-electron cores (Ge, As). This basis set has
a double-zeta -41G contraction for its valence orbitals, to which was added a d
function (exponent 0.207) and additional s (exponent 0.0205) and p (exponent
0.011) functions; the 6-31G** (GeH2 and AsH2+) and
6-31++G** (GaH2-) bases[39,40] were used for hydrogen
atoms in these third-row dihydrides.
References
(1) Miller, J. A. Cancer Res. 1970, 30, 559.